Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 trang 68, 69, 70 sách Kết nối tri thức của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập trong sách giáo khoa.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho các em những bài giải chính xác, khoa học và phù hợp với từng đối tượng học sinh.
Vẽ đường tròn tâm O có bán kính bằng 2cm và dây cung AB có độ dài bằng 2cm. Lấy một điểm C tùy ý nằm trên cung lớn AmB (H.9.2). a) Cho biết số đo góc ở tâm AOB và số đo của cung bị chắn AB. b) Đo góc ACB và so sánh với kết quả của bạn bên cạnh. c) Lấy điểm D tùy ý nằm trên cung ACB. Đo góc ADB và so sánh với các góc ACB và AOB.
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 70 SGK Toán 9 Kết nối tri thức
Hãy cho biết số đo góc nội tiếp tìm được trong Hình 9.3 ở Ví dụ 1, biết rằng số đo của các cung màu xanh trong hình đều bằng \({120^o}\).
Phương pháp giải:
Vì B là góc nội tiếp trong đường tròn nên có số đo bằng nửa số đo cung bị chắn, từ đó tính được góc B.
Lời giải chi tiết:
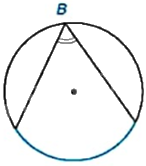
Vì B là góc nội tiếp trong đường tròn nên \(\widehat B = \frac{1}{2}{.120^o} = {60^o}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập trang 70 SGK Toán 9 Kết nối tri thức
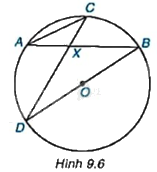
Cho đường tròn tâm O và hai dây cung AB, CD cắt nhau tại điểm X nằm trong đường tròn (H.9.6). Chứng minh rằng $\Delta AXC\backsim \Delta DXB$.
Phương pháp giải:
+ Sử dụng định lí về mối quan hệ giữa góc nội tiếp và cung bị chắn để chứng minh \(\widehat {ACX} = \widehat {XBD}\).
+ Chứng minh $\Delta AXC\backsim \Delta DXB$ theo trường hợp góc – góc.
Lời giải chi tiết:
Vì góc ACX và góc XBD là góc nội tiếp cùng chắn cung AD của đường tròn tâm O nên: \(\widehat {ACX} = \widehat {XBD}\).
Tam giác AXC và tam giác DXB có: \(\widehat {ACX} = \widehat {XBD}\) (cmt), \(\widehat {AXC} = \widehat {BXD}\) (hai góc đối đỉnh).
Do đó, $\Delta AXC\backsim \Delta DXB$ (g – g).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng trang 70SGK Toán 9 Kết nối tri thức
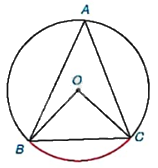
Trở lại tình huống mở đầu, hãy tính số đo của góc BAC nếu đường tròn có bán kính 2cm và dây cung \(BC = 2\sqrt 2 cm\).
Chúng ta đã biết số đo góc ở tâm BOC của đường tròn (O) trong Hình 9.1 bằng số đo của cung bị chắn.
Phương pháp giải:
+ Theo định lí Pythagore đảo chứng minh được tam giác BOC vuông tại O, tính được góc BOC.
+ Vì góc BOC và góc BAC lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung BC của đường tròn (O) nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC}\).
Lời giải chi tiết:
Vì B, C thuộc đường tròn (O) nên \(OB = OC = 2cm\).
Xét tam giác BOC có: \(O{B^2} + O{C^2} = B{C^2}\left( {do\;{2^2} + {2^2} = {{\left( {2\sqrt 2 } \right)}^2}} \right)\) nên tam giác BOC vuông tại O (định lí Pythagore đảo).
Suy ra, \(\widehat {BOC} = {90^o}\)
Vì góc BOC và góc BAC lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung BC của đường tròn (O) nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2}{.90^o} = {45^o}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động trang 68SGK Toán 9 Kết nối tri thức
Vẽ đường tròn tâm O có bán kính bằng 2cm và dây cung AB có độ dài bằng 2cm. Lấy một điểm C tùy ý nằm trên cung lớn AmB (H.9.2).
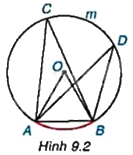
a) Cho biết số đo góc ở tâm AOB và số đo của cung bị chắn AB.
b) Đo góc ACB và so sánh với kết quả của bạn bên cạnh.
c) Lấy điểm D tùy ý nằm trên cung ACB. Đo góc ADB và so sánh với các góc ACB và AOB.
Phương pháp giải:
a) Chứng minh tam giác AOB đều, suy ra \(\widehat {AOB} = {60^o}\). Do đó, \(sđ\overset\frown{AB}=\widehat{AOB}={{60}^{o}}\) (góc ở tâm chắn cung AB).
b, c) Sử dụng thước đo góc đo được góc ACB, góc ADB đều bằng 30 độ. Do đó, \(\widehat {ACB} = \widehat {ADB}\)
Lời giải chi tiết:
Vì A, B thuộc đường tròn tâm O nên \(OA = OB = 2cm\).
Tam giác AOB có: \(OA = OB = AB = 2cm\) nên tam giác ABO đều.
Do đó, \(\widehat {AOB} = {60^o}\).
Suy ra: \(sđ\overset\frown{AB}=\widehat{AOB}={{60}^{o}}\) (góc ở tâm chắn cung AB).
b) Sử dụng thước đo góc, ta đo được \(\widehat {ACB} = {30^o}\).
c) Sử dụng thước đo góc, ta đo được \(\widehat {ADB} = {30^o}\). Do đó, \(\widehat {ADB} = \widehat {ACB}\) và \(\widehat {ADB} = \frac{1}{2}\widehat {AOB}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động trang 68SGK Toán 9 Kết nối tri thức
Vẽ đường tròn tâm O có bán kính bằng 2cm và dây cung AB có độ dài bằng 2cm. Lấy một điểm C tùy ý nằm trên cung lớn AmB (H.9.2).
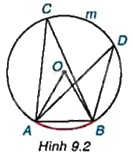
a) Cho biết số đo góc ở tâm AOB và số đo của cung bị chắn AB.
b) Đo góc ACB và so sánh với kết quả của bạn bên cạnh.
c) Lấy điểm D tùy ý nằm trên cung ACB. Đo góc ADB và so sánh với các góc ACB và AOB.
Phương pháp giải:
a) Chứng minh tam giác AOB đều, suy ra \(\widehat {AOB} = {60^o}\). Do đó, \(sđ\overset\frown{AB}=\widehat{AOB}={{60}^{o}}\) (góc ở tâm chắn cung AB).
b, c) Sử dụng thước đo góc đo được góc ACB, góc ADB đều bằng 30 độ. Do đó, \(\widehat {ACB} = \widehat {ADB}\)
Lời giải chi tiết:
Vì A, B thuộc đường tròn tâm O nên \(OA = OB = 2cm\).
Tam giác AOB có: \(OA = OB = AB = 2cm\) nên tam giác ABO đều.
Do đó, \(\widehat {AOB} = {60^o}\).
Suy ra: \(sđ\overset\frown{AB}=\widehat{AOB}={{60}^{o}}\) (góc ở tâm chắn cung AB).
b) Sử dụng thước đo góc, ta đo được \(\widehat {ACB} = {30^o}\).
c) Sử dụng thước đo góc, ta đo được \(\widehat {ADB} = {30^o}\). Do đó, \(\widehat {ADB} = \widehat {ACB}\) và \(\widehat {ADB} = \frac{1}{2}\widehat {AOB}\).
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 70 SGK Toán 9 Kết nối tri thức
Hãy cho biết số đo góc nội tiếp tìm được trong Hình 9.3 ở Ví dụ 1, biết rằng số đo của các cung màu xanh trong hình đều bằng \({120^o}\).
Phương pháp giải:
Vì B là góc nội tiếp trong đường tròn nên có số đo bằng nửa số đo cung bị chắn, từ đó tính được góc B.
Lời giải chi tiết:
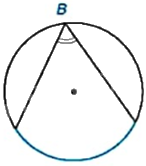
Vì B là góc nội tiếp trong đường tròn nên \(\widehat B = \frac{1}{2}{.120^o} = {60^o}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập trang 70 SGK Toán 9 Kết nối tri thức
Cho đường tròn tâm O và hai dây cung AB, CD cắt nhau tại điểm X nằm trong đường tròn (H.9.6). Chứng minh rằng $\Delta AXC\backsim \Delta DXB$.
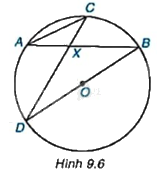
Phương pháp giải:
+ Sử dụng định lí về mối quan hệ giữa góc nội tiếp và cung bị chắn để chứng minh \(\widehat {ACX} = \widehat {XBD}\).
+ Chứng minh $\Delta AXC\backsim \Delta DXB$ theo trường hợp góc – góc.
Lời giải chi tiết:
Vì góc ACX và góc XBD là góc nội tiếp cùng chắn cung AD của đường tròn tâm O nên: \(\widehat {ACX} = \widehat {XBD}\).
Tam giác AXC và tam giác DXB có: \(\widehat {ACX} = \widehat {XBD}\) (cmt), \(\widehat {AXC} = \widehat {BXD}\) (hai góc đối đỉnh).
Do đó, $\Delta AXC\backsim \Delta DXB$ (g – g).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng trang 70SGK Toán 9 Kết nối tri thức
Trở lại tình huống mở đầu, hãy tính số đo của góc BAC nếu đường tròn có bán kính 2cm và dây cung \(BC = 2\sqrt 2 cm\).
Chúng ta đã biết số đo góc ở tâm BOC của đường tròn (O) trong Hình 9.1 bằng số đo của cung bị chắn.
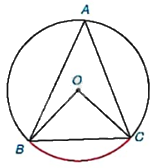
Phương pháp giải:
+ Theo định lí Pythagore đảo chứng minh được tam giác BOC vuông tại O, tính được góc BOC.
+ Vì góc BOC và góc BAC lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung BC của đường tròn (O) nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC}\).
Lời giải chi tiết:
Vì B, C thuộc đường tròn (O) nên \(OB = OC = 2cm\).
Xét tam giác BOC có: \(O{B^2} + O{C^2} = B{C^2}\left( {do\;{2^2} + {2^2} = {{\left( {2\sqrt 2 } \right)}^2}} \right)\) nên tam giác BOC vuông tại O (định lí Pythagore đảo).
Suy ra, \(\widehat {BOC} = {90^o}\)
Vì góc BOC và góc BAC lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung BC của đường tròn (O) nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2}{.90^o} = {45^o}\).
Chương trình Toán 9 tập 2 Kết nối tri thức tập trung vào việc củng cố và mở rộng các kiến thức đã học ở tập 1, đồng thời giới thiệu các chủ đề mới như hàm số bậc hai, hệ phương trình bậc hai, và các ứng dụng của toán học trong thực tế. Trang 68, 69, 70 của sách giáo khoa tập trung vào một số bài tập cụ thể, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết.
Trang 68 thường chứa các bài tập về việc xác định hệ số của hàm số bậc hai, vẽ đồ thị hàm số, và tìm tọa độ giao điểm của đồ thị với các trục tọa độ. Để giải các bài tập này, học sinh cần nắm vững các khái niệm về hàm số bậc hai, phương trình bậc hai, và các phương pháp vẽ đồ thị.
Trang 69 thường chứa các bài tập về việc giải phương trình bậc hai, tìm nghiệm của phương trình, và ứng dụng phương trình bậc hai để giải các bài toán thực tế. Để giải các bài tập này, học sinh cần nắm vững các công thức nghiệm của phương trình bậc hai, điều kiện để phương trình có nghiệm, và các phương pháp giải phương trình.
Trang 70 thường chứa các bài tập tổng hợp, đòi hỏi học sinh phải vận dụng kiến thức của cả chương để giải quyết. Các bài tập này thường có tính ứng dụng cao, giúp học sinh hiểu rõ hơn về tầm quan trọng của toán học trong cuộc sống.
| Bài tập | Nội dung |
|---|---|
| Bài 7 | Tìm giá trị của tham số m để phương trình có nghiệm. |
| Bài 8 | Giải bài toán về quỹ đạo của vật được ném lên. |
| Bài 9 | Chứng minh một biểu thức đại số. |
| Lưu ý: Đây chỉ là ví dụ về nội dung các bài tập, nội dung cụ thể có thể khác nhau tùy theo sách giáo khoa. | |
Để giải bài tập Toán 9 tập 2 trang 68, 69, 70 hiệu quả, các em cần:
Hy vọng với những hướng dẫn chi tiết và lời khuyên trên, các em sẽ tự tin giải quyết các bài tập Toán 9 tập 2 trang 68, 69, 70 Kết nối tri thức một cách hiệu quả. Chúc các em học tập tốt!