Bài tập 4.30 trang 82 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Đây là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 4.30 này, giúp các em học sinh hiểu rõ phương pháp giải và tự tin hơn trong quá trình học tập.
Đố vui. Chu vi Trái Đất bằng bao nhiêu? Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau: 1. Hồi đó, hằng năm cứ vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng. 2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-l
Đề bài
Đố vui. Chu vi Trái Đất bằng bao nhiêu?
Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau:
1. Hồi đó, hằng năm cứ vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng.
2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-lếch-xăng-đri-a) cách Syene 800 km, Eratosthenes thấy 1 tháp cao 25 m có bóng trên mặt đất dài 3,1 m.
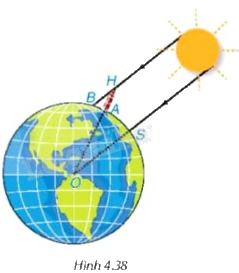
Từ hai quan sát trên, ông có thể tính xấp xỉ “chu vi” của Trái Đất như thế nào? (trên Hình 4.38), điểm O là tâm của Trái Đất, điểm S tượng trưng cho thành phố Syene, điểm A tượng trưng cho thành phố Alexandria, điểm H là đỉnh của tháp, bóng của tháp trên mặt đất được coi là đoạn thẳng AB.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Vẽ hình minh họa để dễ quan sát.
+ Vì đường thẳng vuông góc mặt đất thì đi qua tâm O nên theo giả thiết, tia sáng mặt trời song song với OS, do đó BH song song với OS, suy ra \(\widehat {AHB} = \widehat {AOS}\).
+ Vì \(AH = 25m\) khá bé so với R, Earthostene coi đoạn thẳng \(AB = 3,1m\) vuông góc với AH tạo thành tam giác BAH vuông tại A, ta có \(\tan \widehat {AHB} = \frac{{AB}}{{AH}}\) nên tính được góc SOA.
+ Độ dài một đoạn tùy ý trên đường tròn tâm O tỉ lệ thuận với số góc tạo bởi O và hai đầu mút của đoạn đó nên ta viết được tỉ lệ giữa một đoạn và chu vi đường tròn = tỉ lệ giữa góc tạo thành và \(360^\circ\)
Lời giải chi tiết
Ta có hình minh họa các điểm để dễ quan sát như sau:
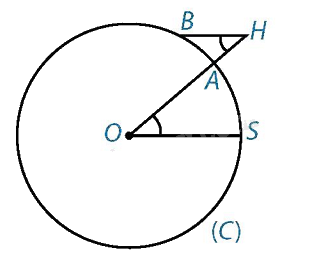
Trên hình vẽ, ta có đường tròn (C) với O là tâm Trái Đất. Đường tròn đi qua S (Syene), A (Alexandria), OS = OA = R.
Theo giả thiết ta có đoạn SA = 800 km.
Gọi H là đỉnh tháp, chân tại A thì A nằm giữa O và H, \(AH = 25m\). Bóng của tháp là đoạn AB.
Vì đường thẳng vuông góc mặt đất thì đi qua tâm O nên theo giả thiết, tia sáng mặt trời song song với OS, do đó BH song song với OS, suy ra \(\widehat {AHB} = \widehat {AOS}\).
Vì \(AH = 25m\) khá bé so với R, Earthostene coi AB là một đoạn thẳng \(AB = 3,1m\) vuông góc với AH tạo thành tam giác BAH vuông tại A, ta có \(\tan \widehat {AHB} = \frac{{AB}}{{AH}} = \frac{{3,1}}{{25}} = \frac{{31}}{{250}}\)
Suy ra \(\tan \widehat {AOS} = \frac{{31}}{{250}}\) nên \(\widehat {AOS} \approx {7^o 4'}\)
Ta có độ dài một đoạn tùy ý trên đường tròn tâm O tỉ lệ thuận với số góc tạo bởi O và hai đầu mút của đoạn đó.
Mà khoảng cách giữa A và S bằng 800km ứng với góc \(\widehat {AOS} \approx {7^o 4'}\) và toàn bộ đường tròn (C) ứng với góc \({360^o}\) nên ta có: \(\frac{C}{800} = \frac{360^o}{7^o 4'}\)
Suy ra chu vi xấp xỉ bằng:
\(C = \frac{{360^o}}{7^o 4'}.800 \approx 40\;755\left( {km} \right)\).
Bài tập 4.30 trang 82 SGK Toán 9 tập 1 yêu cầu chúng ta giải một bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Trước khi đi vào giải bài tập cụ thể, chúng ta cần phân tích đề bài để xác định rõ các yếu tố quan trọng. Bài toán thường cho chúng ta một số thông tin về mối quan hệ giữa hai đại lượng, và yêu cầu chúng ta tìm ra hàm số bậc nhất biểu diễn mối quan hệ đó.
(Nội dung lời giải chi tiết bài tập 4.30 sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng từng bước, và kết luận.)
Ví dụ, giả sử bài toán yêu cầu tìm hàm số bậc nhất y = ax + b đi qua hai điểm A(1; 2) và B(2; 5). Chúng ta sẽ thực hiện như sau:
Ngoài bài tập 4.30, còn rất nhiều bài tập tương tự yêu cầu chúng ta vận dụng kiến thức về hàm số bậc nhất. Một số dạng bài tập thường gặp bao gồm:
Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:
Bài tập 4.30 trang 82 SGK Toán 9 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!