Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2 Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài toán phức tạp.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức Toán 9, tự tin giải quyết các bài tập và đạt kết quả tốt nhất trong học tập.
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 114SGK Toán 9 Kết nối tri thức
Giải các phương trình sau:
a) \({x^2} - 4x + 10 = 0\);
b) \(x + \frac{9}{{x - 1}} = 7\);
c) \({x^2} - 2\left( {\sqrt 3 - 1} \right)x - 2\sqrt 3 = 0\);
d) \(\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} = \frac{4}{{{x^2} - 1}}\).
Phương pháp giải:
+ Để giải phương trình nói chung, ta dùng lệnh Solve (<phương trình>) hoặc Solutions (<phương trình>) trên ô lệnh của cửa sổ CAS kết quả sẽ hiển thị ngay bên dưới.
+ Nghiệm của phương trình được biểu diễn dưới dạng tập hợp. Chú ý, kí hiệu {} thể hiện phương trình vô nghiệm.
Lời giải chi tiết:
a)
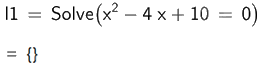
Vậy phương trình \({x^2} - 4x + 10 = 0\) vô nghiệm.
b)
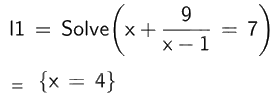
Vậy phương trình \(x + \frac{9}{{x - 1}} = 7\) có nghiệm \(x = 4\).
c)
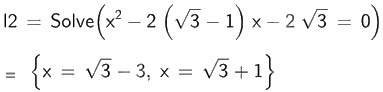
Vậy phương trình \({x^2} - 2\left( {\sqrt 3 - 1} \right)x - 2\sqrt 3 = 0\) có nghiệm \(x = \sqrt 3 - 3;x = \sqrt 3 + 1\).
d)
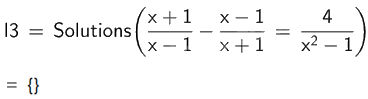
Vậy phương trình \(\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} = \frac{4}{{{x^2} - 1}}\) vô nghiệm.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 114 SGK Toán 9 Kết nối tri thức
Cho đường thẳng \(\left( d \right):y = 2x + \sqrt 3 \) và parabol \(\left( P \right):y = {x^2}\).
a) Vẽ đường thẳng (d) và parabol (P) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (d) và (P).
Phương pháp giải:
- Khởi động GeoGebra và chọn đồng thời hai chế độ Graphic 2 và CAS để vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) và hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\)
+ Nhập công thức hàm số \(y = a{x^2}\) và \(y = ax + b\) vào từng ô lệnh trong cửa sổ CAS.
+ Nháy chuột chọn nút  ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.
ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.
- Sử dụng câu lệnh Intersect ({<phương trình thứ nhất>, (<phương trình thứ hai>}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng.
Lời giải chi tiết:
a) Nhập
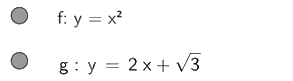
Ta được đồ thị
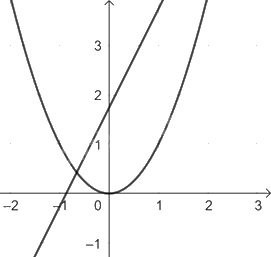
b)
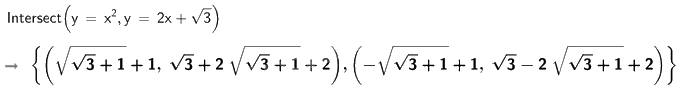
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 114SGK Toán 9 Kết nối tri thức
Giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}3x - 2y = 4\\2x + y = 5\end{array} \right.\);
b) \(\left\{ \begin{array}{l}x + y = 5\\3x + \sqrt[3]{3}y = 6\end{array} \right.\);
c) \(\left\{ \begin{array}{l}3x + 2y = 0\\2x - 3y = 0\end{array} \right.\);
d) \(\left\{ \begin{array}{l}x\sqrt 5 - \left( {1 + \sqrt 3 } \right)y = 1\\\left( {1 - \sqrt 3 } \right)x + y\sqrt 5 = 1\end{array} \right.\).
Phương pháp giải:
Cách 1: Sử dụng câu lệnh Solve ({<phương trình thứ nhất>, (<phương trình thứ hai>}, {<biến số thứ nhất>, (<biến số thứ hai>}) hoặc Solutions ({<phương trình thứ nhất>, (<phương trình thứ hai>}, {<biến số thứ nhất>, (<biến số thứ hai>}) trên ô lệnh của cửa sổ CAS kết quả sẽ hiển thị ngay bên dưới.
Cách 2: Sử dụng câu lệnh Intersect ({<phương trình thứ nhất>, (<phương trình thứ hai>}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng.
Lời giải chi tiết:
a)
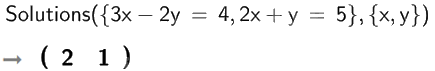
Vậy hệ phương trình \(\left\{ \begin{array}{l}3x - 2y = 4\\2x + y = 5\end{array} \right.\) có nghiệm \(x = 2;y = 1\).
b)
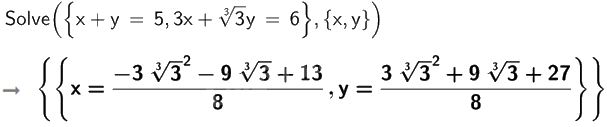
Vậy hệ phương trình \(\left\{ \begin{array}{l}x + y = 5\\3x + \sqrt[3]{3}y = 6\end{array} \right.\) có nghiệm \(x = \frac{{ - 3{{\sqrt[3]{3}}^2} - 9\sqrt[3]{3} + 13}}{8};y = \frac{{3{{\sqrt[3]{3}}^2} + 9\sqrt[3]{3} + 27}}{8}\).
c)
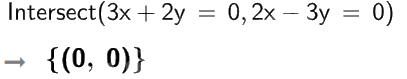
Vậy hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 0\\2x - 3y = 0\end{array} \right.\) có nghiệm \(x = 0;y = 0\).
d)
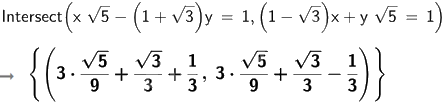
Vậy hệ phương trình \(\left\{ \begin{array}{l}x\sqrt 5 - \left( {1 + \sqrt 3 } \right)y = 1\\\left( {1 - \sqrt 3 } \right)x + y\sqrt 5 = 1\end{array} \right.\) có nghiệm \(x = \frac{{\sqrt 5 }}{3} + \frac{{\sqrt 3 }}{3} + \frac{1}{3};y = \frac{{\sqrt 5 }}{3} + \frac{{\sqrt 3 }}{3} - \frac{1}{3}\).
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 114SGK Toán 9 Kết nối tri thức
Giải các phương trình sau:
a) \({x^2} - 4x + 10 = 0\);
b) \(x + \frac{9}{{x - 1}} = 7\);
c) \({x^2} - 2\left( {\sqrt 3 - 1} \right)x - 2\sqrt 3 = 0\);
d) \(\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} = \frac{4}{{{x^2} - 1}}\).
Phương pháp giải:
+ Để giải phương trình nói chung, ta dùng lệnh Solve (<phương trình>) hoặc Solutions (<phương trình>) trên ô lệnh của cửa sổ CAS kết quả sẽ hiển thị ngay bên dưới.
+ Nghiệm của phương trình được biểu diễn dưới dạng tập hợp. Chú ý, kí hiệu {} thể hiện phương trình vô nghiệm.
Lời giải chi tiết:
a)
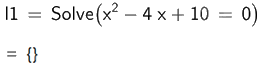
Vậy phương trình \({x^2} - 4x + 10 = 0\) vô nghiệm.
b)
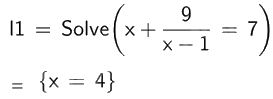
Vậy phương trình \(x + \frac{9}{{x - 1}} = 7\) có nghiệm \(x = 4\).
c)
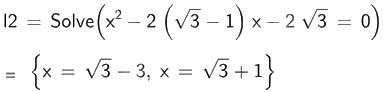
Vậy phương trình \({x^2} - 2\left( {\sqrt 3 - 1} \right)x - 2\sqrt 3 = 0\) có nghiệm \(x = \sqrt 3 - 3;x = \sqrt 3 + 1\).
d)
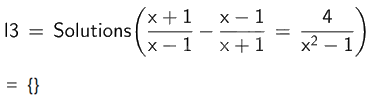
Vậy phương trình \(\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} = \frac{4}{{{x^2} - 1}}\) vô nghiệm.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 114SGK Toán 9 Kết nối tri thức
Giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}3x - 2y = 4\\2x + y = 5\end{array} \right.\);
b) \(\left\{ \begin{array}{l}x + y = 5\\3x + \sqrt[3]{3}y = 6\end{array} \right.\);
c) \(\left\{ \begin{array}{l}3x + 2y = 0\\2x - 3y = 0\end{array} \right.\);
d) \(\left\{ \begin{array}{l}x\sqrt 5 - \left( {1 + \sqrt 3 } \right)y = 1\\\left( {1 - \sqrt 3 } \right)x + y\sqrt 5 = 1\end{array} \right.\).
Phương pháp giải:
Cách 1: Sử dụng câu lệnh Solve ({<phương trình thứ nhất>, (<phương trình thứ hai>}, {<biến số thứ nhất>, (<biến số thứ hai>}) hoặc Solutions ({<phương trình thứ nhất>, (<phương trình thứ hai>}, {<biến số thứ nhất>, (<biến số thứ hai>}) trên ô lệnh của cửa sổ CAS kết quả sẽ hiển thị ngay bên dưới.
Cách 2: Sử dụng câu lệnh Intersect ({<phương trình thứ nhất>, (<phương trình thứ hai>}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng.
Lời giải chi tiết:
a)
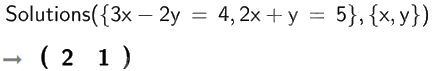
Vậy hệ phương trình \(\left\{ \begin{array}{l}3x - 2y = 4\\2x + y = 5\end{array} \right.\) có nghiệm \(x = 2;y = 1\).
b)
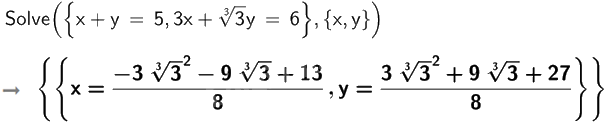
Vậy hệ phương trình \(\left\{ \begin{array}{l}x + y = 5\\3x + \sqrt[3]{3}y = 6\end{array} \right.\) có nghiệm \(x = \frac{{ - 3{{\sqrt[3]{3}}^2} - 9\sqrt[3]{3} + 13}}{8};y = \frac{{3{{\sqrt[3]{3}}^2} + 9\sqrt[3]{3} + 27}}{8}\).
c)
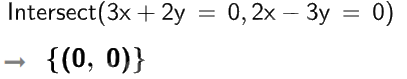
Vậy hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 0\\2x - 3y = 0\end{array} \right.\) có nghiệm \(x = 0;y = 0\).
d)
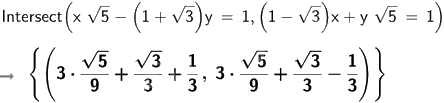
Vậy hệ phương trình \(\left\{ \begin{array}{l}x\sqrt 5 - \left( {1 + \sqrt 3 } \right)y = 1\\\left( {1 - \sqrt 3 } \right)x + y\sqrt 5 = 1\end{array} \right.\) có nghiệm \(x = \frac{{\sqrt 5 }}{3} + \frac{{\sqrt 3 }}{3} + \frac{1}{3};y = \frac{{\sqrt 5 }}{3} + \frac{{\sqrt 3 }}{3} - \frac{1}{3}\).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 114 SGK Toán 9 Kết nối tri thức
Cho đường thẳng \(\left( d \right):y = 2x + \sqrt 3 \) và parabol \(\left( P \right):y = {x^2}\).
a) Vẽ đường thẳng (d) và parabol (P) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (d) và (P).
Phương pháp giải:
- Khởi động GeoGebra và chọn đồng thời hai chế độ Graphic 2 và CAS để vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) và hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\)
+ Nhập công thức hàm số \(y = a{x^2}\) và \(y = ax + b\) vào từng ô lệnh trong cửa sổ CAS.
+ Nháy chuột chọn nút  ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.
ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.
- Sử dụng câu lệnh Intersect ({<phương trình thứ nhất>, (<phương trình thứ hai>}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng.
Lời giải chi tiết:
a) Nhập
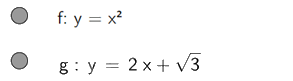
Ta được đồ thị
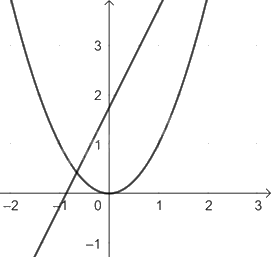
b)
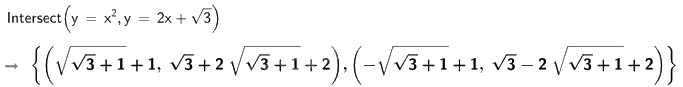
Trang 114 SGK Toán 9 tập 2 Kết nối tri thức chứa các bài tập liên quan đến chủ đề hàm số bậc hai. Đây là một trong những chủ đề quan trọng của chương trình Toán 9, đòi hỏi học sinh phải nắm vững các khái niệm về hàm số, đồ thị hàm số, và các phương pháp giải phương trình bậc hai.
Các bài tập trên trang 114 tập trung vào việc:
Bài 1 yêu cầu học sinh xác định các hệ số a, b, c của các hàm số bậc hai cho trước. Để làm được bài này, học sinh cần nắm vững định nghĩa của hàm số bậc hai và biết cách nhận biết các hệ số a, b, c.
Ví dụ: Cho hàm số y = 2x2 - 3x + 1. Ta có a = 2, b = -3, c = 1.
Bài 2 yêu cầu học sinh tìm tọa độ đỉnh của parabol. Đỉnh của parabol là điểm thấp nhất (hoặc cao nhất) trên đồ thị hàm số. Để tìm đỉnh của parabol, học sinh có thể sử dụng công thức:
xđỉnh = -b / 2a
yđỉnh = -Δ / 4a (với Δ = b2 - 4ac)
Bài 3 yêu cầu học sinh vẽ đồ thị hàm số bậc hai. Để vẽ đồ thị hàm số, học sinh cần xác định các điểm đặc biệt trên đồ thị, như đỉnh, trục đối xứng, giao điểm với trục hoành và trục tung.
Các bước vẽ đồ thị hàm số:
Bài 4 yêu cầu học sinh giải các bài toán thực tế liên quan đến hàm số bậc hai. Các bài toán này thường liên quan đến việc tìm quỹ đạo của một vật thể, hoặc tối ưu hóa một giá trị nào đó.
Ngoài SGK Toán 9 tập 2 Kết nối tri thức, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với những hướng dẫn chi tiết trên, các bạn học sinh sẽ tự tin giải quyết các bài tập trang 114 SGK Toán 9 tập 2 Kết nối tri thức. Chúc các bạn học tập tốt!