Bài tập 6.21 trang 20 SGK Toán 9 tập 2 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế liên quan đến ứng dụng của hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 6.21 trang 20 SGK Toán 9 tập 2 - Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Từ một tấm tôn hình vuông, người ta cắt bỏ bốn hình vuông có độ dài cạnh 8cm ở bốn góc, sau đó gập thành một chiếc thùng có dạng hình hộp chữ nhật không có nắp và có thể tích là (200c{m^3}). Tính độ dài cạnh của tấm tôn hình vuông ban đầu.
Đề bài
Từ một tấm tôn hình vuông, người ta cắt bỏ bốn hình vuông có độ dài cạnh 8cm ở bốn góc, sau đó gập thành một chiếc thùng có dạng hình hộp chữ nhật không có nắp và có thể tích là \(200c{m^3}\). Tính độ dài cạnh của tấm tôn hình vuông ban đầu.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Gọi độ dài cạnh miếng tôn hình vuông ban đầu là x, đặt điều kiện.
+ Tính các kích thước của hình hộp chữ nhật theo x.
+ Tính thể tích của hình hộp chữ nhật theo x.
+ Lập phương trình ẩn về thể tích theo x, giải phương trình, đối chiếu điều kiện và đưa ra kết luận.
Lời giải chi tiết
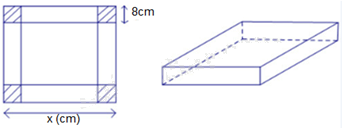
Gọi độ dài cạnh của tấm tôn ban đầu là x (cm, \(x > 16\)).
Khi cắt bỏ bốn hình vuông có độ dài cạnh 8cm ở bốn góc và gập lại, thu được một hình hộp chữ nhật có độ dài các cạnh đáy lần lượt là \(x - 16;x - 16\) và chiều cao là 8cm.
Do đó, thể tích của hình hộp chữ nhật là: \(8{\left( {x - 16} \right)^2}\;\left( {c{m^3}} \right)\)
Mà thể tích của hình hộp chữ nhật là \(200c{m^3}\) nên ta có: \(8{\left( {x - 16} \right)^2} = 200\)
\({\left( {x - 16} \right)^2} = 25\)
\(x - 16 = 5\) hoặc \(x - 16 = - 5\)
\(x = 21\left( {tm} \right)\) hoặc \(x = 11\left( {ktm} \right)\)
Vậy độ dài của cạnh hình vuông ban đầu là 21cm.
Bài tập 6.21 trang 20 SGK Toán 9 tập 2 - Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Nội dung bài tập 6.21:
Một người đi xe đạp từ A đến B với vận tốc 12km/h. Hỏi người đó đi hết bao lâu nếu quãng đường AB dài 36km?
Lời giải:
Gọi t là thời gian người đó đi từ A đến B (t tính bằng giờ).
Quãng đường AB là 36km, vận tốc của người đi xe đạp là 12km/h. Ta có công thức:
Quãng đường = Vận tốc × Thời gian
36 = 12 × t
t = 36 / 12
t = 3
Vậy người đó đi hết 3 giờ để đi từ A đến B.
Phân tích bài toán:
Bài toán này là một bài toán ứng dụng thực tế về hàm số bậc nhất. Trong bài toán này, quãng đường là hàm số của thời gian, vận tốc là hệ số của hàm số. Việc giải bài toán này giúp học sinh hiểu rõ hơn về ứng dụng của hàm số bậc nhất trong thực tế.
Các bài tập tương tự:
Để củng cố kiến thức về hàm số bậc nhất và ứng dụng của nó, các em học sinh có thể làm thêm các bài tập tương tự sau:
Kết luận:
Bài tập 6.21 trang 20 SGK Toán 9 tập 2 - Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc nhất. Việc giải bài tập này giúp học sinh hiểu rõ hơn về ứng dụng của hàm số bậc nhất trong thực tế và rèn luyện kỹ năng giải toán.
Hàm số bậc nhất là một trong những khái niệm quan trọng trong chương trình Toán 9. Ngoài việc giải các bài tập ứng dụng, các em học sinh cũng cần nắm vững các kiến thức lý thuyết về hàm số bậc nhất, bao gồm:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập 6.21 trang 20 SGK Toán 9 tập 2 - Kết nối tri thức, các em học sinh sẽ học tập tốt môn Toán 9 và đạt kết quả cao trong các kỳ thi.
| Công thức | Mô tả |
|---|---|
| Quãng đường = Vận tốc × Thời gian | Công thức tính quãng đường khi biết vận tốc và thời gian. |
| Thời gian = Quãng đường / Vận tốc | Công thức tính thời gian khi biết quãng đường và vận tốc. |