Bài tập 9.24 trang 89 SGK Toán 9 tập 2 thuộc chương trình Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng về hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định hệ số a, b, c của hàm số, tìm đỉnh của parabol, và vẽ đồ thị hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.24 trang 89 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Trong các hình phẳng sau (H.9.52), hình nào là hình phẳng có dạng đa giác đều?
Đề bài
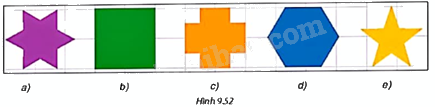
Trong các hình phẳng sau (H.9.52), hình nào là hình phẳng có dạng đa giác đều?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Lời giải chi tiết
Hình phẳng có dạng đa giác đều là: b, d vì các hình này có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Bài tập 9.24 SGK Toán 9 tập 2 Kết nối tri thức yêu cầu học sinh xét hàm số y = x2 - 4x + 3. Bài toán này bao gồm nhiều phần nhỏ, đòi hỏi học sinh nắm vững kiến thức về hàm số bậc hai, đặc biệt là các yếu tố như hệ số a, b, c, đỉnh của parabol, trục đối xứng và giao điểm với các trục tọa độ.
Hàm số y = x2 - 4x + 3 là hàm số bậc hai với:
Việc xác định đúng các hệ số này là bước đầu tiên và quan trọng để giải quyết các phần tiếp theo của bài toán.
Tọa độ đỉnh của parabol y = ax2 + bx + c được tính theo công thức:
Áp dụng vào bài toán, ta có:
Vậy, tọa độ đỉnh của parabol là (2; -1).
Trục đối xứng của parabol là đường thẳng có phương trình x = xđỉnh. Trong trường hợp này, trục đối xứng là x = 2.
Giao điểm của parabol với trục hoành là nghiệm của phương trình y = 0, tức là x2 - 4x + 3 = 0.
Ta có thể giải phương trình này bằng cách sử dụng công thức nghiệm của phương trình bậc hai:
x = (-b ± √Δ) / 2a
Với Δ = 4 (đã tính ở trên), ta có:
Vậy, parabol cắt trục hoành tại hai điểm A(1; 0) và B(3; 0).
Giao điểm của parabol với trục tung là điểm có hoành độ x = 0. Thay x = 0 vào phương trình hàm số, ta được:
y = 02 - 4 * 0 + 3 = 3
Vậy, parabol cắt trục tung tại điểm C(0; 3).
Dựa vào các thông tin đã tìm được (đỉnh, trục đối xứng, giao điểm với các trục tọa độ), ta có thể vẽ được đồ thị hàm số y = x2 - 4x + 3.
Đồ thị là một parabol có đỉnh tại (2; -1), trục đối xứng là x = 2, cắt trục hoành tại A(1; 0) và B(3; 0), cắt trục tung tại C(0; 3).
Bài tập 9.24 trang 89 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán điển hình về hàm số bậc hai. Việc nắm vững các kiến thức về hệ số, đỉnh, trục đối xứng và giao điểm của parabol là rất quan trọng để giải quyết bài toán này một cách chính xác và hiệu quả. Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải quyết bài tập và hiểu sâu hơn về hàm số bậc hai.
Ngoài ra, các em có thể tham khảo thêm các bài tập tương tự và các tài liệu học tập khác trên giaitoan.edu.vn để nâng cao kiến thức và kỹ năng giải toán.