Chào mừng bạn đến với bài học lý thuyết Mở đầu về đường tròn trong chương trình Toán 9 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về đường tròn, nền tảng cho việc giải các bài toán liên quan.
Chúng ta sẽ cùng nhau khám phá định nghĩa đường tròn, các yếu tố liên quan như tâm, bán kính, đường kính, và các khái niệm quan trọng khác. Giaitoan.edu.vn cam kết mang đến cho bạn một trải nghiệm học tập hiệu quả và thú vị.
1. Đường tròn
1. Đường tròn
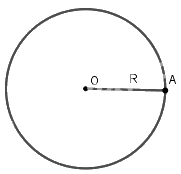
Định nghĩa đường tròn
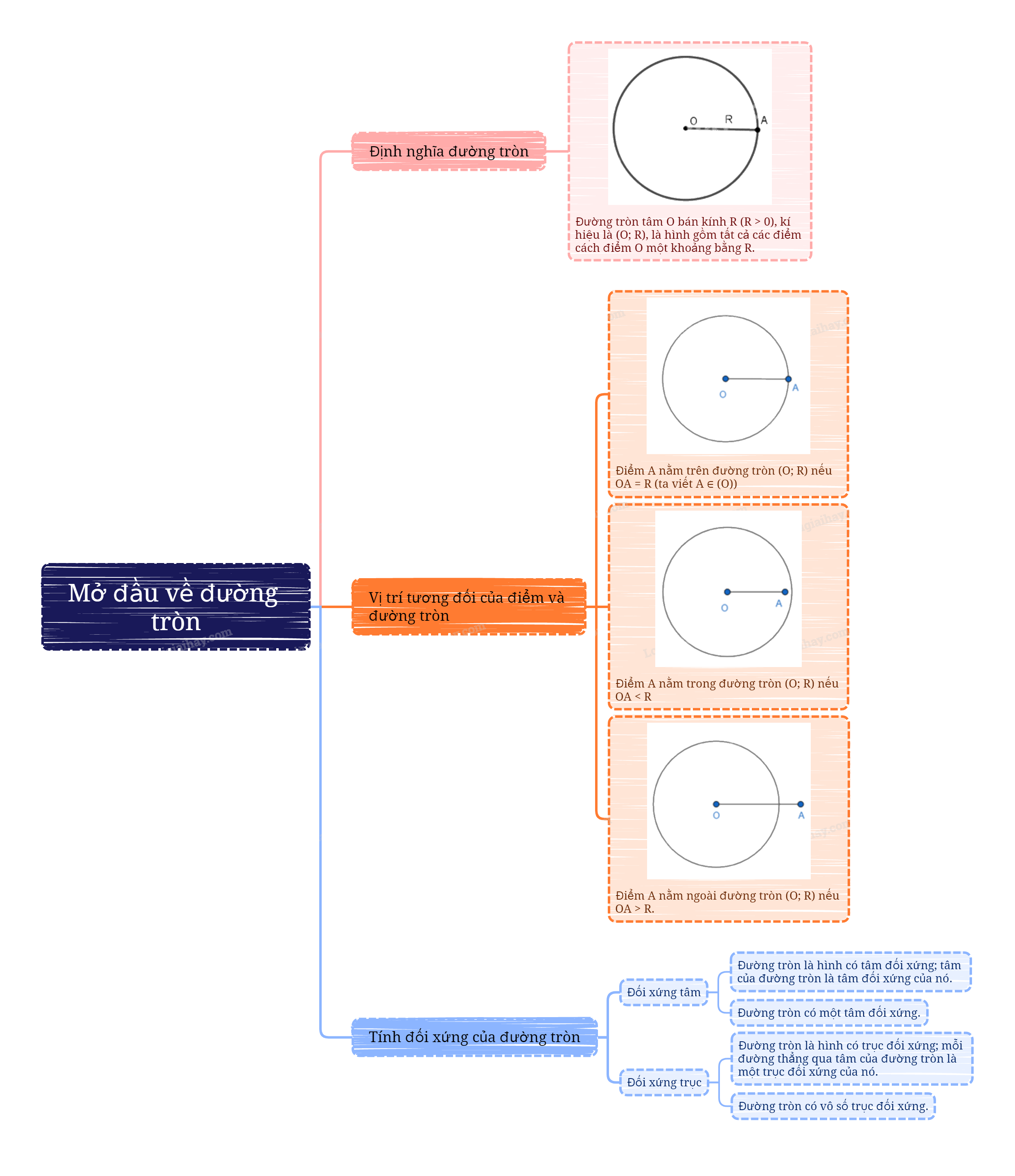
Đường tròn tâm O bán kính R (R > 0), kí hiệu là (O; R), là hình gồm tất cả các điểm cách điểm O một khoảng bằng R. |
Khi không cần để ý đến bán kính ta kí hiệu đường tròn tâm O là (O).
Điểm thuộc đường tròn
Nếu A là một điểm của đường tròn (O) thì ta viết \(A \in \left( O \right)\). Khi đó, ta còn nói đường tròn (O) đi qua điểm A, hay điểm A nằm trên đường tròn (O).
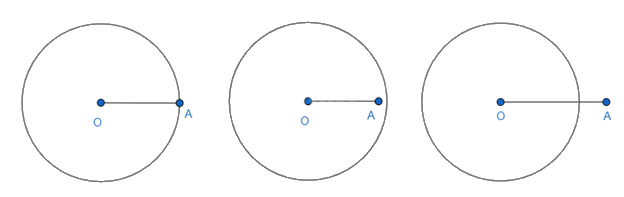
Tổng quát:
- Điểm A nằm trên đường tròn (O; R) nếu OA = R;
- Điểm A nằm trong đường tròn (O; R) nếu OA < R;
- Điểm A nằm ngoài đường tròn (O; R) nếu OA > R.
Hình tròn tâm O bán kính R là hình gồm các điểm nằm trên và nằm trong đường tròn (O;R).
2. Tính đối xứng của đường tròn
a) Đối xứng tâm
Hai điểm M và M’ gọi là đối xứng với nhau qua điểm I (hay qua tâm I) nếu I là trung điểm của đoạn MM’.

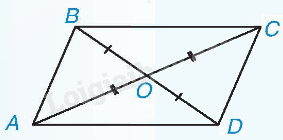
Ví dụ: Nếu O là giao điểm của hai đường chéo của hình bình hành ABCD thì
+) OA = OC nên A và C đối xứng với nhau.
+) OB = OD nên B và D đối xứng với nhau.
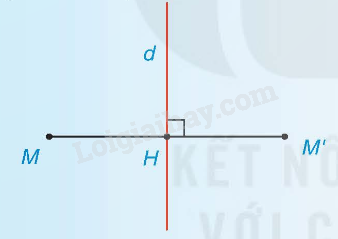
b) Đối xứng trục
Hai điểm M và M’ gọi là đối xứng với nhau qua đường thẳng d (hay qua trục d) nếu d là đường trung trực của đoạn MM’.
Ví dụ: Nếu AH là đường cao trong tam giác ABC cân tại A thì AH cũng là đường trung trực của BC, nên B và C đối xứng với nhau qua AH.
c) Tâm đối xứng của đường tròn
- Đường tròn là hình có tâm đối xứng; tâm của đường tròn là tâm đối xứng của nó. - Đường tròn có một tâm đối xứng. |
d) Trục đối xứng của đường tròn
- Đường tròn là hình có trục đối xứng; mỗi đường thẳng qua tâm của đường tròn là một trục đối xứng của nó. - Đường tròn có vô số trục đối xứng. |
Bài học này sẽ đi sâu vào các khái niệm cơ bản về đường tròn, một trong những hình học quan trọng nhất trong chương trình Toán 9 Kết nối tri thức. Việc nắm vững lý thuyết này là nền tảng để giải quyết các bài toán phức tạp hơn liên quan đến đường tròn trong các chương tiếp theo.
Đường tròn là tập hợp tất cả các điểm nằm trên một mặt phẳng, cách đều một điểm cố định gọi là tâm của đường tròn. Khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn được gọi là bán kính (R) của đường tròn.
Chu vi (C) của đường tròn được tính bằng công thức:
C = 2πR hoặc C = πd
Diện tích (S) của đường tròn được tính bằng công thức:
S = πR2
Xét một điểm A nằm trên mặt phẳng chứa đường tròn (O; R). Ta có ba trường hợp:
Đường tròn nội tiếp đa giác đều: Là đường tròn tiếp xúc với tất cả các cạnh của đa giác đều. Tâm của đường tròn nội tiếp là giao điểm của các đường phân giác của các góc của đa giác đều.
Đường tròn ngoại tiếp đa giác đều: Là đường tròn đi qua tất cả các đỉnh của đa giác đều. Tâm của đường tròn ngoại tiếp là giao điểm của các đường trung trực của các cạnh của đa giác đều.
Ví dụ 1: Một đường tròn có bán kính 5cm. Tính chu vi và diện tích của đường tròn đó.
Giải:
Chu vi: C = 2πR = 2 * 3.14159 * 5 = 31.4159 cm
Diện tích: S = πR2 = 3.14159 * 52 = 78.53975 cm2
Ví dụ 2: Cho một đường tròn (O; 3cm). Điểm A cách O một khoảng 2cm. Hỏi điểm A nằm bên trong, bên ngoài hay trên đường tròn?
Giải:
Vì OA = 2cm < 3cm = R nên điểm A nằm bên trong đường tròn.
Để nắm vững kiến thức về lý thuyết Mở đầu về đường tròn, bạn nên thực hành giải nhiều bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về đường tròn. Chúc bạn học tập tốt!