Bài tập 5.9 trang 94 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Đây là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 5.9, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho đường tròn (O; 4 cm) và ba điểm A, B, C trên đường tròn đó sao cho tam giác ABC cân tại đỉnh A và số đo của cung nhỏ BC bằng (70^circ .) a) Giải thích tại sao hai cung nhỏ AB và AC bằng nhau. b) Tính độ dài của các cung BC, AB và AC (làm tròn kết quả đến hàng phần mười).
Đề bài
Cho đường tròn (O; 4 cm) và ba điểm A, B, C trên đường tròn đó sao cho tam giác ABC cân tại đỉnh A và số đo của cung nhỏ BC bằng \(70^\circ .\)
a) Giải thích tại sao hai cung nhỏ AB và AC bằng nhau.
b) Tính độ dài của các cung BC, AB và AC (làm tròn kết quả đến hàng phần mười).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Xét \(\Delta OAB\) và \(\Delta OAC\) từ đó suy ra\(\widehat {AOB} = \widehat {AOC}\)
b) Tính số đo cung AB và AC, sau đó áp dụng công thức tính độ dài cung.
Lời giải chi tiết
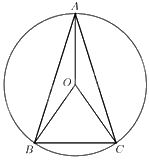
a) Xét \(\Delta OAB\) và \(\Delta OAC\) có:
OA chung
OA = OC = R
AB = AC (do \(\Delta ABC\) cân tại A)
\(\Rightarrow \Delta OAB=\Delta OAC\) (c.c.c)
\(\Rightarrow \widehat{AOB}=\widehat{AOC}\)(hai góc tương ứng)
\(\Rightarrow \) sđ\(\overset\frown{AB}=\) sđ \(\overset\frown{AC}\)
\(\Rightarrow \overset\frown{AB}=\overset\frown{AC}\)
b) Độ dài cung BC là:
\(\frac{{70}}{{180}}.\pi .4 = \frac{{14}}{9}\pi \approx \frac{{14}}{9}.3,14 \approx 4,9 \)(cm)
Ta có: \(\widehat {AOB} + \widehat {AOC} + \widehat {BOC} = 360^\circ \)
\(\begin{array}{l} \Rightarrow 2.\widehat {AOB} + 70^\circ = 360^\circ \\ \Rightarrow 2.\widehat {AOB}\,\, = 290^\circ \\ \Rightarrow \,\,\,\,\,\,\widehat {AOB}\,\, = 145^\circ \end{array}\)
Độ dài cung AB và cung AC là: \(\frac{{145}}{{180}}.\pi .4 = \frac{{29}}{9}\pi \approx \frac{{29}}{9}.3,14 \approx 10,1 \)(cm)
Bài tập 5.9 yêu cầu chúng ta giải quyết một bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Trước khi đi vào giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Bài tập 5.9 thường đưa ra một tình huống thực tế, ví dụ như mối quan hệ giữa quãng đường đi được và thời gian, hoặc giữa số lượng sản phẩm và doanh thu. Chúng ta cần xác định được các biến số và mối quan hệ giữa chúng để xây dựng hàm số bậc nhất.
Dưới đây là lời giải chi tiết bài tập 5.9 trang 94 SGK Toán 9 tập 1 - Kết nối tri thức. (Nội dung lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu tìm hàm số bậc nhất biểu diễn mối quan hệ giữa nhiệt độ C (độ C) và nhiệt độ F (độ F). Biết rằng khi C = 0 thì F = 32, và khi C = 100 thì F = 212.
Để nắm vững kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài tập, các em có thể thực hiện các bài tập sau:
Ngoài bài tập 5.9, các em có thể tìm hiểu thêm về các ứng dụng của hàm số bậc nhất trong thực tế, ví dụ như trong kinh tế, vật lý, hoặc kỹ thuật. Việc hiểu rõ các ứng dụng này sẽ giúp các em thấy được tầm quan trọng của kiến thức Toán học trong cuộc sống.
Bài tập 5.9 trang 94 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và hướng dẫn của Giaitoan.edu.vn, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức Toán học. Chúc các em học tập tốt!