Bài tập 4.1 trang 73 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để xác định hệ số góc và vẽ đồ thị hàm số. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, đầy đủ và dễ tiếp thu nhất, giúp các em học sinh có thể tự học và ôn tập hiệu quả.
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, cosin, tang, cotang của các góc nhọn B và C khi biết: a) AB = 8 cm, BC = 17 cm; b) AC = 0,9 cm, AB = 1,2 cm.
Đề bài
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, cosin, tang, cotang của các góc nhọn B và C khi biết:
a) AB = 8 cm, BC = 17 cm;
b) AC = 0,9 cm, AB = 1,2 cm.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng các tỉ số lượng giác để giải.
Lời giải chi tiết
a)
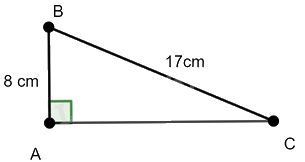
Tam giác ABC vuông tại A nên ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Thay số ta có \({17^2} = {8^2} + A{C^2}\) hay \(A{C^2} = {17^2} - {8^2} = 225\) suy ra \(AC = 15\) cm (vì \(AC > 0\))
Ta có: \(\sin \widehat B = \cos \widehat C = \frac{{AC}}{{BC}} = \frac{{15}}{{17}}\)
\(\cos \widehat B = \sin \widehat C = \frac{{AB}}{{BC}} = \frac{8}{{17}}\)
\(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{{15}}{8}\)
\(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{8}{{15}}\)
b)
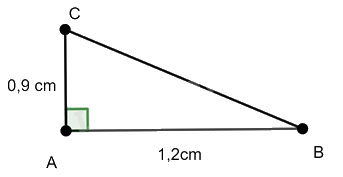
Tam giác ABC vuông tại A nên ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Thay số ta có \(B{C^2} = 1,{2^2} + 0,{9^2} = 2,25\) hay \(CB = \sqrt {2,25} = 1,5\) cm (vì \(BC > 0\))
Ta có: \(\sin \widehat B = \cos \widehat C = \frac{{AC}}{{BC}} = \frac{{0,9}}{{1,5}} = \frac{3}{5}\)
\(\cos \widehat B = \sin \widehat C = \frac{{AB}}{{BC}} = \frac{{1,2}}{{1,5}} = \frac{4}{5}\)
\(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{{0,9}}{{1,2}} = \frac{3}{4}\)
\(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{{1,2}}{{0,9}} = \frac{4}{3}\)
Bài tập 4.1 trang 73 SGK Toán 9 tập 1 yêu cầu học sinh xác định hệ số góc của đường thẳng và vẽ đồ thị hàm số. Để giải bài tập này, chúng ta cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, bao gồm:
Nội dung bài tập 4.1:
Cho hàm số y = (m - 1)x + 3. Tìm giá trị của m để hàm số là hàm số bậc nhất và đồ thị của hàm số song song với đường thẳng y = 2x - 1.
Để hàm số y = (m - 1)x + 3 là hàm số bậc nhất, điều kiện cần và đủ là m - 1 ≠ 0, tức là m ≠ 1.
Đồ thị của hàm số y = (m - 1)x + 3 song song với đường thẳng y = 2x - 1 khi và chỉ khi hệ số góc của hai đường thẳng bằng nhau. Do đó, ta có:
m - 1 = 2
Giải phương trình trên, ta được m = 3.
Vậy, với m = 3, hàm số y = (m - 1)x + 3 là hàm số bậc nhất và đồ thị của hàm số song song với đường thẳng y = 2x - 1.
Giả sử m = 3, ta có hàm số y = 2x + 3. Để vẽ đồ thị hàm số này, ta có thể xác định hai điểm thuộc đồ thị, chẳng hạn:
Nối hai điểm A và B lại với nhau, ta được đồ thị của hàm số y = 2x + 3.
Để củng cố kiến thức về hàm số bậc nhất và cách vẽ đồ thị hàm số, các em có thể tự giải các bài tập sau:
Bài tập 4.1 trang 73 SGK Toán 9 tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và cách vẽ đồ thị hàm số. Hy vọng với lời giải chi tiết và ví dụ minh họa trên, các em học sinh có thể tự giải bài tập này một cách dễ dàng và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!