Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 2 trang 70 SGK Toán 9 tập 1 - Kết nối tri thức. Bài viết này cung cấp đáp án đầy đủ, dễ hiểu, cùng với phương pháp giải bài tập hiệu quả, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Cho tam giác ABC vuông tại C, có (widehat A = alpha ,widehat B = beta ) (H.4.9) . Hãy viết các tỉ số lượng giác của góc (alpha ,beta ) theo độ dài các cạnh của tam giác ABC. Trong các tỉ số đó, cho biết các cặp tỉ số bằng nhau.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 70 SGK Toán 9 Kết nối tri thức
Hãy giải thích tại sao \(\sin {35^0} = \cos {55^0},\tan {35^0} = \cot {55^0}.\)
Phương pháp giải:
Nếu hai góc phụ nhau (tổng số đo hai góc bằng \({90^0}\)) thì sin góc này bằng cosin góc kia, tan góc này bằng cot góc kia.
Lời giải chi tiết:
Vì \({35^0} + {55^0} = {90^0}\) nên \(\sin {35^0} = \cos {55^0},\tan {35^0} = \cot {55^0}.\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 70 SGK Toán 9 Kết nối tri thức
Cho tam giác ABC vuông tại C, có \(\widehat A = \alpha ,\widehat B = \beta \) (H.4.9) . Hãy viết các tỉ số lượng giác của góc \(\alpha ,\beta \) theo độ dài các cạnh của tam giác ABC. Trong các tỉ số đó, cho biết các cặp tỉ số bằng nhau.
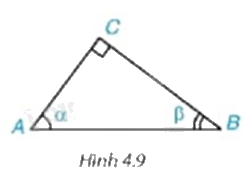
Phương pháp giải:
Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc \(\alpha \), kí hiệu \(\sin \widehat B\)
Tỉ số giữa cạnh kề và cạnh huyền gọi là cosin của góc \(\alpha \), kí hiệu \(\cos \widehat B\)
Tỉ số giữa cạnh đối và cạnh kề của góc \(\alpha \) gọi là \(\tan \widehat \alpha \)
Tỉ số giữa cạnh kề và cạnh đối của góc \(\alpha \) gọi là \(\cot \widehat \alpha \)
Lời giải chi tiết:
Ta có:
\(\sin \alpha = \frac{{BC}}{{AB}};\) \(\cos \alpha = \frac{{AC}}{{AB}};\) \(\tan \alpha = \frac{{BC}}{{AC}};\) \(\cot \alpha = \frac{{AC}}{{BC}}\)
\(\sin \beta = \frac{{AC}}{{AB}};\) \(\cos \beta = \frac{{BC}}{{AB}};\) \(\tan \beta = \frac{{AC}}{{BC}};\) \(\cot \beta = \frac{{BC}}{{AC}}\)
Từ đó ta có
\(\sin \alpha = \cos \beta ;\) \(\cos \alpha = \sin \beta ;\) \(\tan \alpha = \cot \beta ;\) \(\cot \alpha = \tan \beta .\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 70 SGK Toán 9 Kết nối tri thức
Cho tam giác ABC vuông tại C, có \(\widehat A = \alpha ,\widehat B = \beta \) (H.4.9) . Hãy viết các tỉ số lượng giác của góc \(\alpha ,\beta \) theo độ dài các cạnh của tam giác ABC. Trong các tỉ số đó, cho biết các cặp tỉ số bằng nhau.
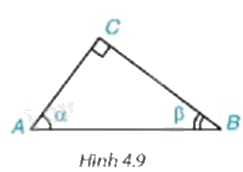
Phương pháp giải:
Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc \(\alpha \), kí hiệu \(\sin \widehat B\)
Tỉ số giữa cạnh kề và cạnh huyền gọi là cosin của góc \(\alpha \), kí hiệu \(\cos \widehat B\)
Tỉ số giữa cạnh đối và cạnh kề của góc \(\alpha \) gọi là \(\tan \widehat \alpha \)
Tỉ số giữa cạnh kề và cạnh đối của góc \(\alpha \) gọi là \(\cot \widehat \alpha \)
Lời giải chi tiết:
Ta có:
\(\sin \alpha = \frac{{BC}}{{AB}};\) \(\cos \alpha = \frac{{AC}}{{AB}};\) \(\tan \alpha = \frac{{BC}}{{AC}};\) \(\cot \alpha = \frac{{AC}}{{BC}}\)
\(\sin \beta = \frac{{AC}}{{AB}};\) \(\cos \beta = \frac{{BC}}{{AB}};\) \(\tan \beta = \frac{{AC}}{{BC}};\) \(\cot \beta = \frac{{BC}}{{AC}}\)
Từ đó ta có
\(\sin \alpha = \cos \beta ;\) \(\cos \alpha = \sin \beta ;\) \(\tan \alpha = \cot \beta ;\) \(\cot \alpha = \tan \beta .\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 70 SGK Toán 9 Kết nối tri thức
Hãy giải thích tại sao \(\sin {35^0} = \cos {55^0},\tan {35^0} = \cot {55^0}.\)
Phương pháp giải:
Nếu hai góc phụ nhau (tổng số đo hai góc bằng \({90^0}\)) thì sin góc này bằng cosin góc kia, tan góc này bằng cot góc kia.
Lời giải chi tiết:
Vì \({35^0} + {55^0} = {90^0}\) nên \(\sin {35^0} = \cos {55^0},\tan {35^0} = \cot {55^0}.\)
Mục 2 trang 70 SGK Toán 9 tập 1 - Kết nối tri thức thường xoay quanh các chủ đề về hàm số bậc nhất, bao gồm việc xác định hàm số, vẽ đồ thị hàm số, và ứng dụng của hàm số trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng cho các chương trình học Toán ở các lớp trên.
Để hiểu rõ hơn về nội dung mục 2 trang 70, chúng ta cần xem xét các phần chính sau:
Dưới đây là một số bài tập minh họa thường gặp trong mục 2 trang 70 SGK Toán 9 tập 1 - Kết nối tri thức, cùng với lời giải chi tiết:
Cho hàm số y = (m - 2)x + 3. Tìm giá trị của m để hàm số là hàm số bậc nhất.
Lời giải:
Để hàm số y = (m - 2)x + 3 là hàm số bậc nhất, thì hệ số của x phải khác 0, tức là m - 2 ≠ 0. Suy ra m ≠ 2.
Vẽ đồ thị hàm số y = 2x - 1.
Lời giải:
Để vẽ đồ thị hàm số y = 2x - 1, ta xác định hai điểm thuộc đồ thị:
Vẽ đường thẳng đi qua hai điểm A(0; -1) và B(1/2; 0), ta được đồ thị hàm số y = 2x - 1.
Một ô tô đi từ A đến B với vận tốc 60km/h. Gọi t là thời gian ô tô đi từ A đến B (t tính bằng giờ). Hãy viết công thức tính quãng đường ô tô đi được theo thời gian t.
Lời giải:
Quãng đường ô tô đi được là s = v.t, trong đó v là vận tốc và t là thời gian. Trong trường hợp này, v = 60km/h. Vậy công thức tính quãng đường ô tô đi được theo thời gian t là s = 60t.
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 70 SGK Toán 9 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!