Giải mục 1 trang 122 SGK Toán 9 tập 2 - Kết nối tri thức

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2 - Kết nối tri thức. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp tối ưu nhất.

Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt trong môn Toán.

Hỏi ý kiến của các bạn trong lớp về địa điểm đi dã ngoại với ba lựa chọn: Tràng An, Ba Vì, Đại Lải thu được kết quả sau: Tràng An, Ba Vì, Tràng An, Tràng An, Ba Vì, Ba Vì, Đại Lải, Tràng An, Tràng An, Ba Vì, Tràng An, Đại Lải, Tràng An, Tràng An, Tràng An, Tràng An, Tràng An, Tràng An, Ba Vì, Đại Lải, Tràng An, Ba Vì, Tràng An, Đại Lải, Ba Vì, Ba Vì, Ba Vì, Ba Vì, Đại Lải, Tràng An. Sử dụng bảng tính Excel, hãy lập bảng tần số, bảng tần số tương đối cho dãy dữ liệu trên và vẽ các biểu đồ cột,

Đề bài

Trả lời câu hỏi Thực hành 1 trang 122SGK Toán 9 Kết nối tri thức

Hỏi ý kiến của các bạn trong lớp về địa điểm đi dã ngoại với ba lựa chọn: Tràng An, Ba Vì, Đại Lải thu được kết quả sau:

Tràng An, Ba Vì, Tràng An, Tràng An, Ba Vì, Ba Vì, Đại Lải, Tràng An, Tràng An, Ba Vì, Tràng An, Đại Lải, Tràng An, Tràng An, Tràng An, Tràng An, Tràng An, Tràng An, Ba Vì, Đại Lải, Tràng An, Ba Vì, Tràng An, Đại Lải, Ba Vì, Ba Vì, Ba Vì, Ba Vì, Đại Lải, Tràng An.

Sử dụng bảng tính Excel, hãy lập bảng tần số, bảng tần số tương đối cho dãy dữ liệu trên và vẽ các biểu đồ cột, biểu đồ hình quạt tròn biểu diễn chúng.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải mục 1 trang 122 SGK Toán 9 tập 2 - Kết nối tri thức 1

Để xác định tần số, tần số tương đối và biểu diễn bằng biểu đồ (biểu đồ cột, biểu đồ hình quạt tròn) từ một dãy dữ liệu dạng liệt kê trong Excel, ta thực hiện các bước sau:

Bước 1. Nhập dữ liệu dạng liệt kê vào một cột trong bảng tính.

Bước 2. Tạo bảng dữ liệu bằng cách xác định vùng dữ liệu và đặt tên cho bảng dữ liệu.

Bước 3. Sử dụng chức năng Pivot Table để tạo bảng tần số, tần số tương đối.

Bước 4. Từ bảng tần số, tần số tương đối vẽ đồ thị biểu diễn.

Lời giải chi tiết

Bước 1. Nhập dữ liệu trên vào vùng dữ liệu A2: A31, ô A1 là tên cột địa điểm đi dã ngoại.

Bước 2.Chọn Insert $ \to $ Table, chọn vùng dữ liệu $A$1: $A$31, tích vào ô My table has headers. Trong ô Table Name đặt tên cho bảng dữ liệu là Diadiemdangoai.

Bước 3. Chọn Insert $ \to $ Pivot Table. Trong ô Table Range điền tên bảng dữ liệu Diadiemdangoai, chọn Existing Worksheet, trong ô Location chọn một vùng dữ liệu bất kì nào đó để đặt bảng kết quả, chẳng hạn ta chọn vùng C2:C5 thì ô này sẽ hiện ra Sheet3!$C$2:$E$5. Chọn OK. Trong bảng Pivot Table Field List, kéo thả trường kết quả vào 2 ô Rowlabels và Values, ta sẽ thu được bảng tần số. Để thu được tần số tương đối của các giá trị, trong ô E3 ta điền $ = D3/ D 6$ và sao chép công thức đến hết ô E5, điền nội dung “Tần số tương đối” vào ô E2 và kiểm tra tổng tần số tương đối bằng cách điền $ = SUM\left( {E3:E5} \right)$ vào ô E6 như hình dưới đây.

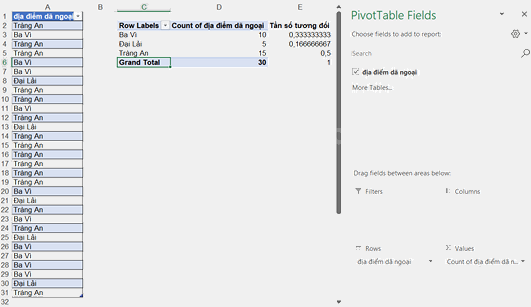
Giải mục 1 trang 122 SGK Toán 9 tập 2 - Kết nối tri thức 2

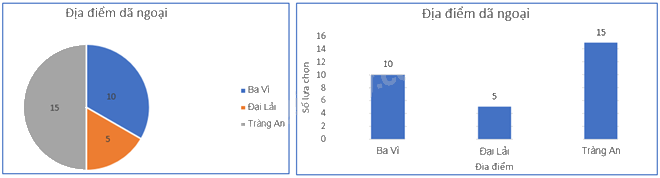
Bước 4. Để vẽ biểu đồ ta chọn vùng dữ liệu C3:D5, sau đó ta chọn vào Insert chọn biểu đồ cột hoặc biểu đồ hình quạt tròn, điền đầy đủ các thông tin cần thiết để hoàn thiện biểu đồ. Kết quả thu được như sau:

Biểu đồ tần số:

Giải mục 1 trang 122 SGK Toán 9 tập 2 - Kết nối tri thức 3

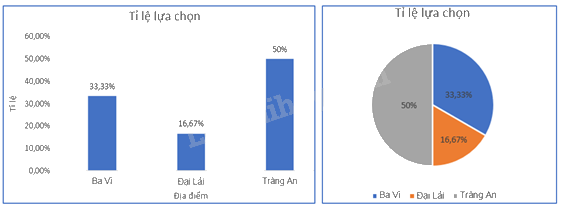
Biểu đồ tần số tương đối

Giải mục 1 trang 122 SGK Toán 9 tập 2 - Kết nối tri thức 4

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải mục 1 trang 122 SGK Toán 9 tập 2 - Kết nối tri thức đặc sắc thuộc chuyên mục bài tập toán 9 trên nền tảng đề thi toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải mục 1 trang 122 SGK Toán 9 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp

Mục 1 trang 122 SGK Toán 9 tập 2 - Kết nối tri thức thường xoay quanh các chủ đề về hàm số bậc hai, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng. Việc nắm vững kiến thức nền tảng về hàm số là vô cùng quan trọng để giải quyết các bài toán liên quan.

1. Các khái niệm cơ bản về hàm số bậc hai

Hàm số bậc hai có dạng tổng quát là y = ax² + bx + c, trong đó a, b, c là các hệ số và a ≠ 0. Để hiểu rõ hơn về hàm số bậc hai, chúng ta cần nắm vững các khái niệm sau:

Hệ số a: Xác định độ lồi hoặc lõm của đồ thị hàm số. Nếu a > 0, đồ thị hàm số có dạng parabol mở lên trên. Nếu a < 0, đồ thị hàm số có dạng parabol mở xuống dưới.
Đỉnh của parabol: Điểm thấp nhất (nếu a > 0) hoặc điểm cao nhất (nếu a < 0) của đồ thị hàm số. Tọa độ đỉnh của parabol được tính bằng công thức: x_đỉnh = -b/2a và y_đỉnh = f(x_đỉnh).
Trục đối xứng của parabol: Đường thẳng x = x_đỉnh.
Giao điểm với trục Oy: Điểm có tọa độ (0, c).
Giao điểm với trục Ox: Các điểm có hoành độ là nghiệm của phương trình ax² + bx + c = 0.

2. Phương pháp giải các bài tập trong Mục 1 trang 122

Để giải các bài tập trong Mục 1 trang 122 SGK Toán 9 tập 2 - Kết nối tri thức một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:

Xác định các hệ số a, b, c: Đây là bước đầu tiên và quan trọng nhất để xác định dạng của hàm số và các tính chất của nó.
Tính tọa độ đỉnh của parabol: Sử dụng công thức x_đỉnh = -b/2a và y_đỉnh = f(x_đỉnh) để tìm tọa độ đỉnh.
Vẽ đồ thị hàm số: Dựa vào các thông tin đã tính được (đỉnh, trục đối xứng, giao điểm với các trục tọa độ) để vẽ đồ thị hàm số.
Sử dụng các tính chất của hàm số: Ví dụ, nếu a > 0, hàm số đồng biến trên khoảng (x_đỉnh, +∞) và nghịch biến trên khoảng (-∞, x_đỉnh).
Giải phương trình bậc hai: Sử dụng công thức nghiệm hoặc phương pháp phân tích thành nhân tử để tìm nghiệm của phương trình ax² + bx + c = 0.

3. Ví dụ minh họa

Bài tập: Xét hàm số y = 2x² - 8x + 6. Hãy tìm tọa độ đỉnh của parabol và vẽ đồ thị hàm số.

Giải:

Xác định hệ số: a = 2, b = -8, c = 6.
Tính tọa độ đỉnh: x_đỉnh = -(-8)/(2*2) = 2; y_đỉnh = 2*(2)² - 8*2 + 6 = -2. Vậy tọa độ đỉnh của parabol là (2, -2).
Vẽ đồ thị: Đồ thị hàm số là một parabol mở lên trên, có đỉnh tại (2, -2) và trục đối xứng là x = 2. Giao điểm với trục Oy là (0, 6). Để tìm giao điểm với trục Ox, ta giải phương trình 2x² - 8x + 6 = 0, được nghiệm x₁ = 1 và x₂ = 3. Vậy giao điểm với trục Ox là (1, 0) và (3, 0).

4. Luyện tập và củng cố kiến thức

Để nắm vững kiến thức về hàm số bậc hai và rèn luyện kỹ năng giải bài tập, bạn nên thực hành giải nhiều bài tập khác nhau từ SGK, sách bài tập và các nguồn tài liệu học tập khác. Đừng ngần ngại tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè nếu gặp khó khăn.

5. Ứng dụng của hàm số bậc hai trong thực tế

Hàm số bậc hai có nhiều ứng dụng trong thực tế, ví dụ như:

Tính quỹ đạo của vật ném: Quỹ đạo của một vật ném lên không trung có dạng parabol.
Thiết kế cầu: Hình dạng của cầu thường được mô tả bằng hàm số bậc hai.
Tối ưu hóa lợi nhuận: Trong kinh tế, hàm số bậc hai có thể được sử dụng để tối ưu hóa lợi nhuận.

Hy vọng rằng với những kiến thức và phương pháp giải bài tập được trình bày ở trên, bạn sẽ tự tin hơn khi đối mặt với các bài tập trong Mục 1 trang 122 SGK Toán 9 tập 2 - Kết nối tri thức. Chúc bạn học tập tốt!