Bài tập 5.37 trang 113 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Đây là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 5.37 này, giúp các em học sinh hiểu rõ phương pháp giải và tự tin hơn trong các bài kiểm tra.
Cho AB là một dây bất kì (không phải là đường kính) của đường tròn (O; 4 cm). Gọi C và D lần lượt là các điểm đối xứng với A và B qua tâm O. a) Hai điểm C và D có nằm trên đường tròn (O) không? Vì sao? b) Biết rằng ABCD là một hình vuông. Tính độ dài cung lớn AB và diện tích hình quạt tròn tạo bởi hai bán kính OA và OB.
Đề bài
Cho AB là một dây bất kì (không phải là đường kính) của đường tròn (O; 4 cm). Gọi C và D lần lượt là các điểm đối xứng với A và B qua tâm O.
a) Hai điểm C và D có nằm trên đường tròn (O) không? Vì sao?
b) Biết rằng ABCD là một hình vuông. Tính độ dài cung lớn AB và diện tích hình quạt tròn tạo bởi hai bán kính OA và OB.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Nếu một điểm thuộc đường tròn (O) thì điểm đối xứng với nó qua tâm O cũng thuộc (O).
b) Tính số đo góc \(\widehat {{\rm{AOB}}}\), rồi suy ra số đo cung lớn AB.
Áp dụng công thức tính độ dài cung và diện tích hình quạt tròn để tính.
Lời giải chi tiết
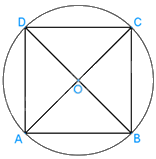
a) A thuộc (O), C là điểm đối xứng của A qua O nên C thuộc (O);
B thuộc (O), D là điểm đối xứng của B qua O nên D thuộc (O).
b) ABCD là hình vuông nên AC và BD vuông góc
Do đó: \(\widehat {{\rm{AOB}}} = 90^\circ \). Suy ra sđ \(\overset\frown{\text{AB}}=90{}^\circ \)
Suy ra: số đo cung lớn AB là: \(360^\circ - 90^\circ = 270^\circ \).
Độ dài cung lớn AB là: \(\frac{n}{{180}}.\pi R = \frac{{270}}{{180}}.4\pi = 6\pi \)(cm)
Diện tích hình quạt tròn tạo bởi hai bán kính OA và OB là:
\(\frac{{\rm{n}}}{{360}}.{\rm{\pi }}{{\rm{R}}^2} = \frac{{90}}{{360}}{\rm{.\pi }}{\rm{.}}{{\rm{4}}^2} = 4{\rm{\pi }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Bài tập 5.37 trang 113 SGK Toán 9 tập 1 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một bài toán thực tế liên quan đến việc xác định hàm số và tính giá trị của hàm số tại một điểm cho trước. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và phương pháp sau:
Đề bài: (Đề bài đầy đủ của bài tập 5.37 cần được chèn vào đây. Ví dụ: Cho hàm số y = 2x + 3. Tính giá trị của y khi x = -1.)
Lời giải:
Để hiểu rõ hơn về cách giải bài tập 5.37, chúng ta hãy xem xét một số ví dụ minh họa sau:
Ngoài ra, các em có thể tự giải các bài tập tương tự để rèn luyện kỹ năng giải toán:
Khi giải bài tập về hàm số bậc nhất, các em cần lưu ý những điều sau:
Bài tập 5.37 trang 113 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất. Hy vọng rằng, với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ phương pháp giải bài tập này và tự tin hơn trong các bài kiểm tra. Chúc các em học tốt!