Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 9 tập 1 - Kết nối tri thức, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 3 trang 101, 102, 103 tập trung vào các kiến thức quan trọng của chương học. Việc hiểu rõ và vận dụng thành thạo các kiến thức này là nền tảng cho các bài học tiếp theo.
Cho điểm M ở bên ngoài một đường tròn tâm O. Hãy dùng thước và compa thực hiện các bước vẽ hình như sau: - Vẽ đường tròn đường kính MO cắt đường tròn (O) tại A và B; - Vẽ và chứng tỏ các đường thẳng MA và MB là hai tiếp tuyến của (O).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 102 SGK Toán 9 Kết nối tri thức
(Dựa vào hình vẽ có được sau HĐ3).
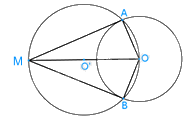
Bằng cách xét hai tam giác OMA và OMB, chứng minh rằng:
a) MA = MB;
b) MO là tia phân giác của góc AMB;
c) OM là tia phân giác của góc AOB.
Phương pháp giải:
Chứng minh \(\Delta {\rm{OAM}} = \Delta {\rm{OBM}}\), từ đó suy ra các cặp cạnh, góc tương ứng bằng nhau.
Lời giải chi tiết:
a) Xét hai tam giác vuông OAM và OBM có:
OA = OB
OM chung
Vậy \(\Delta {\rm{OAM}} = \Delta {\rm{OBM}}\) (cạnh huyền – cạnh góc vuông)
Suy ra: MA = MB (hai cạnh tương ứng)
b) Vì \(\Delta {\rm{OAM}} = \Delta {\rm{OBM}}\) (câu a) nên \(\widehat {{\rm{OAM}}} = \widehat {{\rm{OBM}}}\) (hai góc tương ứng)
Suy ra MO là tia phân giác của góc AMB.
c) Vì \(\Delta {\rm{OAM}} = \Delta {\rm{OBM}}\) (câu a) nên \(\widehat {{\rm{AOM}}} = \widehat {{\rm{BOM}}}\) (hai góc tương ứng)
Suy ra OM là tia phân giác của góc AOB.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 101 SGK Toán 9 Kết nối tri thức
Cho điểm M ở bên ngoài một đường tròn tâm O. Hãy dùng thước và compa thực hiện các bước vẽ hình như sau:
- Vẽ đường tròn đường kính MO cắt đường tròn (O) tại A và B;
- Vẽ và chứng tỏ các đường thẳng MA và MB là hai tiếp tuyến của (O).
Phương pháp giải:
- Lấy trung điểm O’ của OM, vẽ đường tròn tâm O’ bán kính OO’.
- Ta chứng minh MA vuông góc với OA, MB vuông góc với OB.
Lời giải chi tiết:
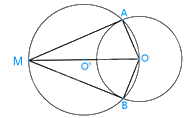
Tam giác OAM có O’A = O’O = O’M (cùng là bán kính của đường tròn (O’)) nên tam giác OAM vuông tại A.
Suy ra: MA\( \bot \)OA tại A hay MA là tiếp tuyến của đường tròn (O’)
Tam giác OBM có O’B = O’O = O’M (cùng là bán kính của đường tròn (O’)) nên tam giác OBM vuông tại B.
Suy ra: MB\( \bot \)OB tại B hay MB là tiếp tuyến của đường tròn (O’)
Video hướng dẫn giải
Trả lời câu hỏi Thử thách nhỏ trang 103 SGK Toán 9 Kết nối tri thức
Cho góc xMy và điểm A thuộc tia Mx. Hãy vẽ đường tròn tâm O tiếp xúc với cả hai cạnh của góc xMy sao cho A là một trong hai tiếp điểm.
Phương pháp giải:
Cần nhớ kiến thức đường phân giác: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đấy.
Đường tròn tiếp xúc với đường thẳng thì khoảng cách từ tâm đến đường thẳng bằng bán kính
Lời giải chi tiết:
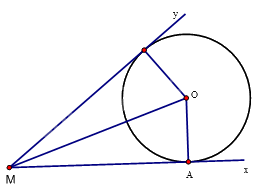
Vẽ góc xMy rồi lấy điểm A trên Mx, để vẽ đường tròn tâm O tiếp xúc với cả hai cạnh của góc xMy thì khoảng cách từ O đến hai tia Mx và My bằng nhau và bằng bán kính của đường tròn nên O thuộc đường phân giác của góc xMy.
Để (O) tiếp xúc với Mx tại A thì OA vuông góc với Mx tại A.
Do đó O là giao điểm của phân giác góc xMy và đường vuông góc với Mx tại A.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 101 SGK Toán 9 Kết nối tri thức
Cho điểm M ở bên ngoài một đường tròn tâm O. Hãy dùng thước và compa thực hiện các bước vẽ hình như sau:
- Vẽ đường tròn đường kính MO cắt đường tròn (O) tại A và B;
- Vẽ và chứng tỏ các đường thẳng MA và MB là hai tiếp tuyến của (O).
Phương pháp giải:
- Lấy trung điểm O’ của OM, vẽ đường tròn tâm O’ bán kính OO’.
- Ta chứng minh MA vuông góc với OA, MB vuông góc với OB.
Lời giải chi tiết:
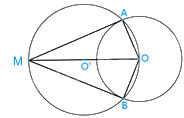
Tam giác OAM có O’A = O’O = O’M (cùng là bán kính của đường tròn (O’)) nên tam giác OAM vuông tại A.
Suy ra: MA\( \bot \)OA tại A hay MA là tiếp tuyến của đường tròn (O’)
Tam giác OBM có O’B = O’O = O’M (cùng là bán kính của đường tròn (O’)) nên tam giác OBM vuông tại B.
Suy ra: MB\( \bot \)OB tại B hay MB là tiếp tuyến của đường tròn (O’)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 102 SGK Toán 9 Kết nối tri thức
(Dựa vào hình vẽ có được sau HĐ3).
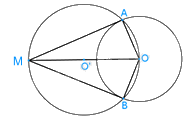
Bằng cách xét hai tam giác OMA và OMB, chứng minh rằng:
a) MA = MB;
b) MO là tia phân giác của góc AMB;
c) OM là tia phân giác của góc AOB.
Phương pháp giải:
Chứng minh \(\Delta {\rm{OAM}} = \Delta {\rm{OBM}}\), từ đó suy ra các cặp cạnh, góc tương ứng bằng nhau.
Lời giải chi tiết:
a) Xét hai tam giác vuông OAM và OBM có:
OA = OB
OM chung
Vậy \(\Delta {\rm{OAM}} = \Delta {\rm{OBM}}\) (cạnh huyền – cạnh góc vuông)
Suy ra: MA = MB (hai cạnh tương ứng)
b) Vì \(\Delta {\rm{OAM}} = \Delta {\rm{OBM}}\) (câu a) nên \(\widehat {{\rm{OAM}}} = \widehat {{\rm{OBM}}}\) (hai góc tương ứng)
Suy ra MO là tia phân giác của góc AMB.
c) Vì \(\Delta {\rm{OAM}} = \Delta {\rm{OBM}}\) (câu a) nên \(\widehat {{\rm{AOM}}} = \widehat {{\rm{BOM}}}\) (hai góc tương ứng)
Suy ra OM là tia phân giác của góc AOB.
Video hướng dẫn giải
Trả lời câu hỏi Thử thách nhỏ trang 103 SGK Toán 9 Kết nối tri thức
Cho góc xMy và điểm A thuộc tia Mx. Hãy vẽ đường tròn tâm O tiếp xúc với cả hai cạnh của góc xMy sao cho A là một trong hai tiếp điểm.
Phương pháp giải:
Cần nhớ kiến thức đường phân giác: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đấy.
Đường tròn tiếp xúc với đường thẳng thì khoảng cách từ tâm đến đường thẳng bằng bán kính
Lời giải chi tiết:
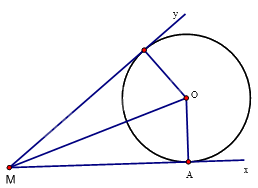
Vẽ góc xMy rồi lấy điểm A trên Mx, để vẽ đường tròn tâm O tiếp xúc với cả hai cạnh của góc xMy thì khoảng cách từ O đến hai tia Mx và My bằng nhau và bằng bán kính của đường tròn nên O thuộc đường phân giác của góc xMy.
Để (O) tiếp xúc với Mx tại A thì OA vuông góc với Mx tại A.
Do đó O là giao điểm của phân giác góc xMy và đường vuông góc với Mx tại A.
Mục 3 trong SGK Toán 9 tập 1 - Kết nối tri thức thường xoay quanh các chủ đề về hàm số bậc nhất, hệ số góc, và ứng dụng của hàm số trong giải quyết các bài toán thực tế. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản, công thức và phương pháp giải.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực. 'a' được gọi là hệ số góc, quyết định độ dốc của đường thẳng biểu diễn hàm số. 'b' là tung độ gốc, là giao điểm của đường thẳng với trục Oy.
Các bài tập trong mục 3 thường yêu cầu học sinh:
Bài 1 (Trang 101): Cho hàm số y = 2x - 3. Tìm các điểm A, B thuộc đồ thị hàm số lần lượt có hoành độ là -2 và 1. Giải: Thay x = -2 vào y = 2x - 3, ta được y = 2*(-2) - 3 = -7. Vậy A(-2; -7). Thay x = 1 vào y = 2x - 3, ta được y = 2*1 - 3 = -1. Vậy B(1; -1).
Bài 2 (Trang 102): Vẽ đồ thị hàm số y = -x + 2. Giải: Để vẽ đồ thị hàm số, ta cần xác định hai điểm thuộc đồ thị. Chọn x = 0, ta được y = 2. Chọn x = 2, ta được y = 0. Vậy đồ thị hàm số là đường thẳng đi qua hai điểm A(0; 2) và B(2; 0).
Bài 3 (Trang 103): Tìm giá trị của m để hàm số y = (m - 1)x + 2 là hàm số bậc nhất. Giải: Để hàm số y = (m - 1)x + 2 là hàm số bậc nhất, thì hệ số của x phải khác 0. Vậy m - 1 ≠ 0, suy ra m ≠ 1.
Để nắm vững kiến thức về hàm số bậc nhất, học sinh nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Việc giải nhiều bài tập sẽ giúp các em hiểu rõ hơn về các khái niệm, công thức và phương pháp giải.
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với những kiến thức và phương pháp giải trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 3 trang 101, 102, 103 SGK Toán 9 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!