Chào mừng bạn đến với bài học về lý thuyết Hình trụ và hình nón trong chương trình Toán 9 Kết nối tri thức. Đây là một trong những chủ đề quan trọng, đòi hỏi sự hiểu biết sâu sắc về các khái niệm và công thức liên quan.
Tại giaitoan.edu.vn, chúng tôi cung cấp một lộ trình học tập rõ ràng, bài giảng chi tiết và bài tập thực hành đa dạng để giúp bạn nắm vững kiến thức một cách hiệu quả nhất.
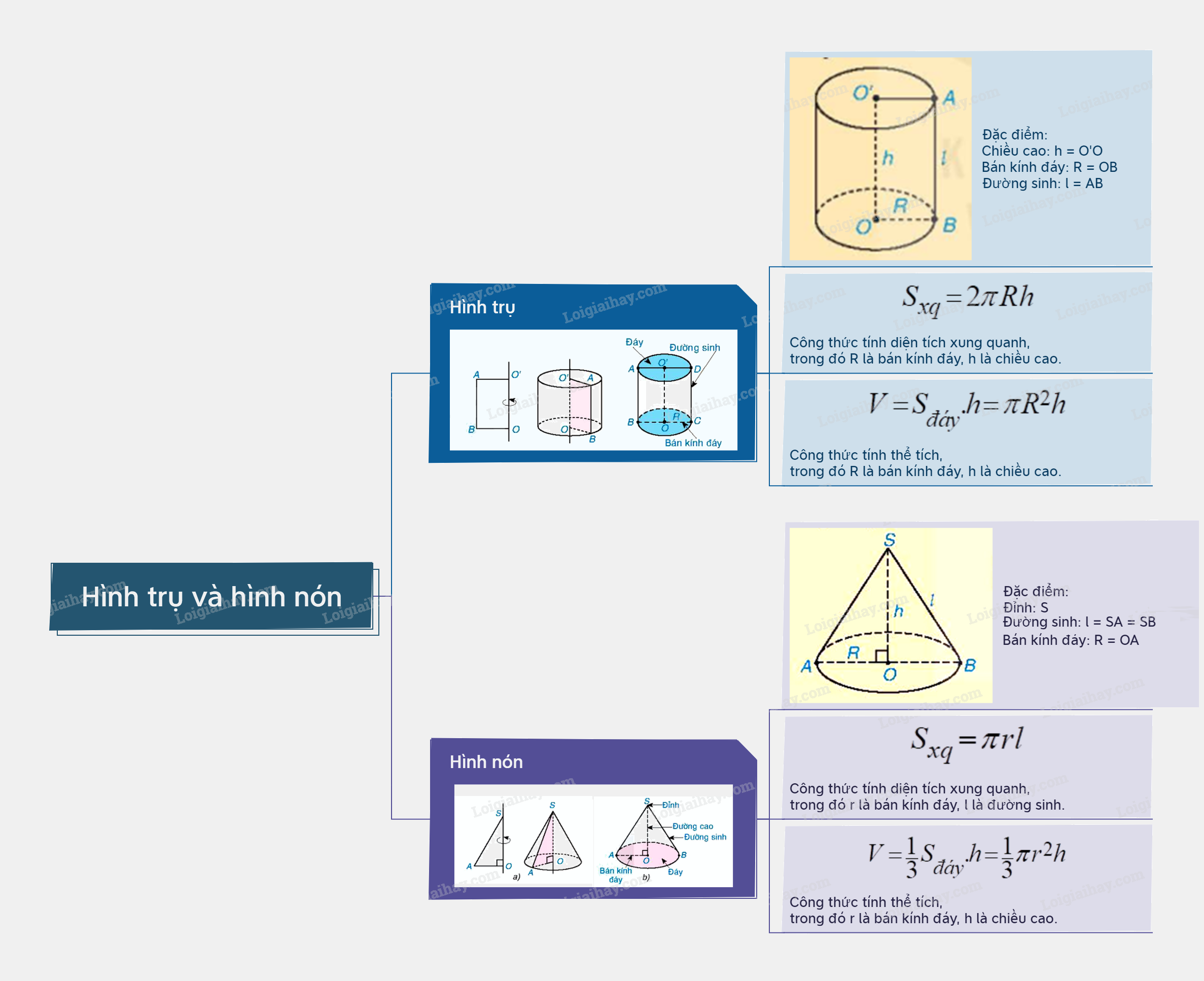
1. Hình trụ Đặc điểm Một số yếu tố của hình trụ: Chiều cao: (h = O'O). Bán kính đáy: (R = OB). Đường sinh: (l = AB).
1. Hình trụ
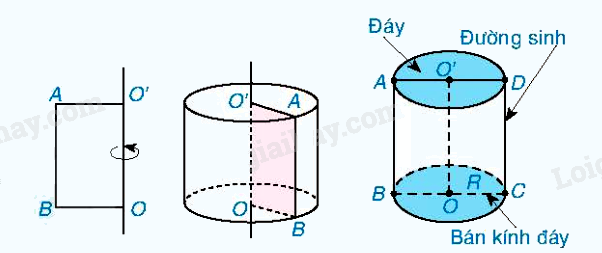
Đặc điểm
Một số yếu tố của hình trụ: Chiều cao: \(h = O'O\). Bán kính đáy: \(R = OB\). Đường sinh: \(l = AB\). |
Diện tích xung quanh của hình trụ
Công thức tính diện tích xung quanh của hình trụ: \({S_{xq}} = 2\pi Rh\), trong đó R là bán kính đáy, h là chiều cao. |
Thể tích của hình trụ
Công thức tính thể tích của hình trụ: \(V = {S_{đáy}}.h = \pi {R^2}h\), trong đó \({S_{đáy}}\) là diện tích đáy, R là bán kính đáy, h là chiều cao. |
Ví dụ:
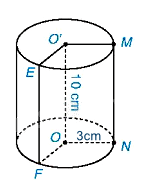
O’M là một bán kính đáy của hình trụ.
EF là một đường sinh của hình trụ.
Chiều cao \(O'O = 10cm\).
Diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi Rh = 2\pi .3.10 = 60\pi \left( {c{m^2}} \right)\)
Diện tích đáy là:
\({S_{đáy}} = \pi {R^2} = \pi {.3^2} = 9\pi \left( {c{m^2}} \right)\)
Thể tích của hình trụ là:
\(V = {S_{đáy}}.h = 9\pi .10 = 90\pi \left( {c{m^3}} \right)\)
2. Hình nón
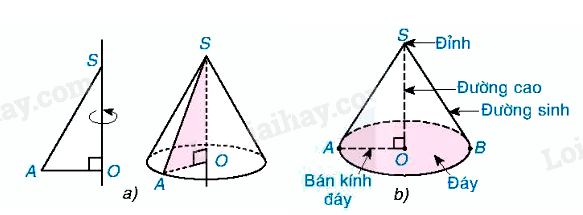
Đặc điểm
Một số yếu tố của hình nón: Đỉnh: S. Chiều cao: \(h = SO\). Đường sinh: \(l = SA = SB\). Bán kính đáy: \(R = OA\). |
Diện tích xung quanh của hình nón
Công thức tính diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\), trong đó r là bán kính đáy, l là độ dài đường sinh. |
Thể tích của hình nón
Công thức tính thể tích của hình nón: \(V = \frac{1}{3}{S_{đáy}}.h = \frac{1}{3}\pi {r^2}h\), trong đó \({S_{đáy}}\) là diện tích đáy, r là bán kính đáy, h là chiều cao. |
Ví dụ:
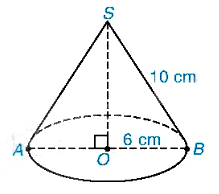
Hình nón có:
- Đỉnh: S.
- Đường cao: SO.
- Bán kính đáy: SA, SB.
- Đường sinh: SA, SB.
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rl = \pi .6.10 = 60\pi \left( {c{m^2}} \right)\).
Tam giác SOB vuông tại O nên theo định lí Pythagore ta có:
\(\begin{array}{l}O{B^2} + S{O^2} = S{B^2}\\{6^2} + S{O^2} = {10^2}\\S{O^2} = 100 - 36 = 64\\SO = 8cm.\end{array}\)
Thể tích của hình nón là \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.8 = 96\pi \left( {c{m^3}} \right)\).
Trong chương trình Toán 9 Kết nối tri thức, kiến thức về hình trụ và hình nón đóng vai trò quan trọng trong việc phát triển tư duy không gian và khả năng giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết, công thức và các ứng dụng của hai hình học này.
1. Định nghĩa: Hình trụ là hình có hai đáy là hai đường tròn bằng nhau và nằm trên hai mặt phẳng song song. Hai đáy này được nối với nhau bằng một mặt bên là mặt trụ.
2. Các yếu tố của hình trụ:
3. Diện tích xung quanh của hình trụ: Diện tích xung quanh của hình trụ được tính bằng công thức: Sxq = 2πrh
4. Diện tích toàn phần của hình trụ: Diện tích toàn phần của hình trụ được tính bằng công thức: Stp = Sxq + 2πr2 = 2πrh + 2πr2
5. Thể tích của hình trụ: Thể tích của hình trụ được tính bằng công thức: V = πr2h
1. Định nghĩa: Hình nón là hình có đáy là một đường tròn và mặt bên là mặt nón.
2. Các yếu tố của hình nón:
3. Mối quan hệ giữa đường sinh, chiều cao và bán kính đáy: l2 = r2 + h2
4. Diện tích xung quanh của hình nón: Diện tích xung quanh của hình nón được tính bằng công thức: Sxq = πrl
5. Diện tích toàn phần của hình nón: Diện tích toàn phần của hình nón được tính bằng công thức: Stp = Sxq + πr2 = πrl + πr2
6. Thể tích của hình nón: Thể tích của hình nón được tính bằng công thức: V = (1/3)πr2h
Ví dụ 1: Một hình trụ có bán kính đáy là 5cm và chiều cao là 10cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ đó.
Giải:
Ví dụ 2: Một hình nón có bán kính đáy là 3cm và chiều cao là 4cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón đó.
Giải:
Khi học về hình trụ và hình nón, bạn cần nắm vững các định nghĩa, công thức và mối quan hệ giữa các yếu tố của hai hình này. Đồng thời, hãy luyện tập thường xuyên với các bài tập khác nhau để củng cố kiến thức và rèn luyện kỹ năng giải toán.
Hãy chú ý đến việc đổi đơn vị đo lường cho phù hợp và kiểm tra lại kết quả sau khi tính toán để đảm bảo tính chính xác.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết Hình trụ và hình nón Toán 9 Kết nối tri thức. Chúc bạn học tập tốt!