Định lí Viète là một trong những kiến thức quan trọng trong chương trình Toán 9, đặc biệt là chương trình Kết nối tri thức. Nắm vững định lí này giúp học sinh giải quyết nhiều bài toán liên quan đến phương trình bậc hai một cách nhanh chóng và hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về Lý thuyết Định lí Viète cùng với các bài tập vận dụng đa dạng, giúp bạn hiểu sâu sắc và áp dụng thành thạo kiến thức này.
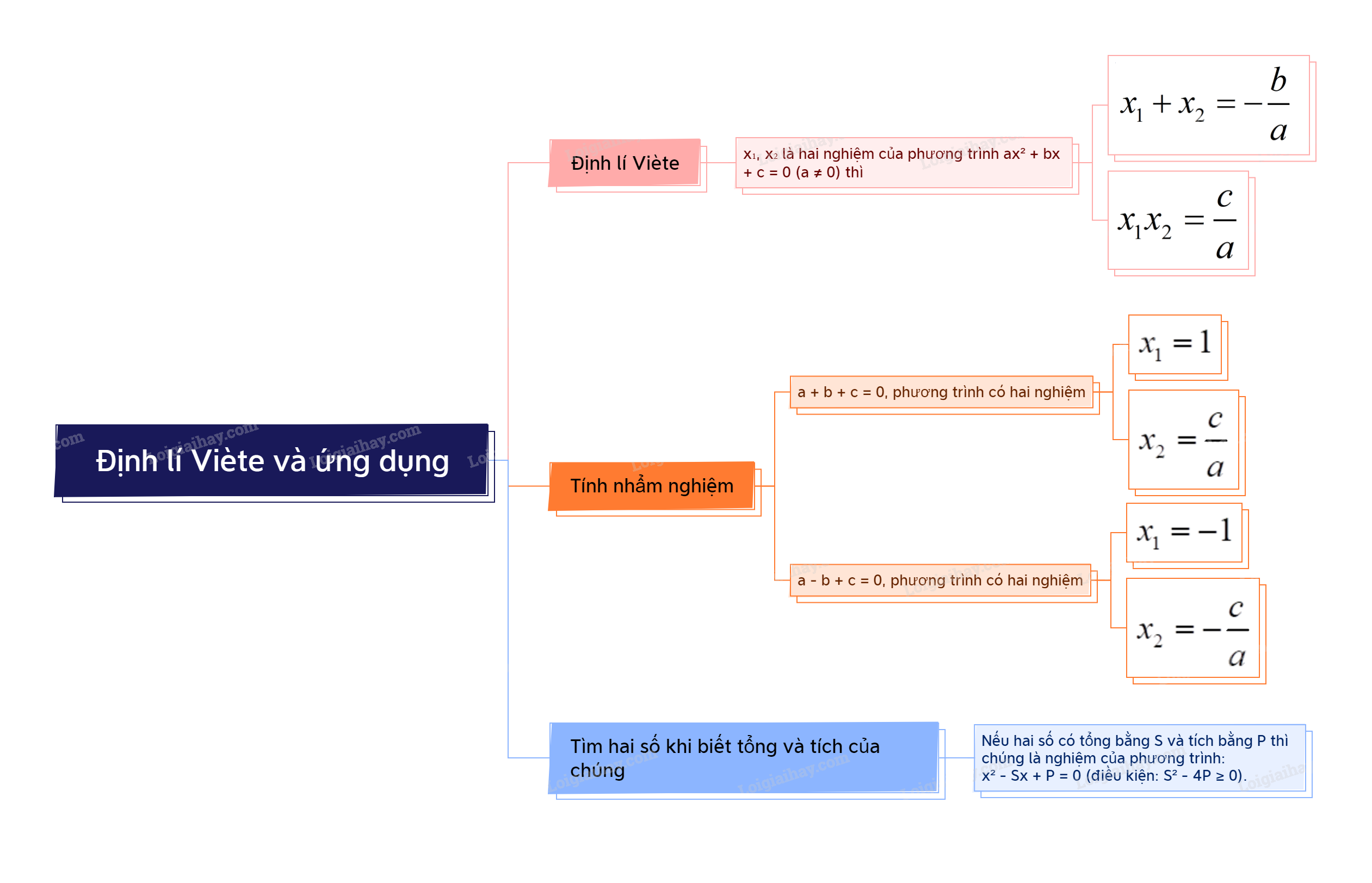
1. Định lí Viète Nếu ({x_1},{x_2}) là hai nghiệm của phương trình (a{x^2} + bx + c = 0left( {a ne 0} right)) thì (left{ begin{array}{l}{x_1} + {x_2} = - frac{b}{a}\{x_1}{x_2} = frac{c}{a}.end{array} right.)
1. Định lí Viète
Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) thì \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}.\end{array} \right.\) |
Ví dụ: Phương trình \(2{x^2} + 11x + 7 = 0\) có: \(\Delta = {11^2} - 4.2.7 = 65 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Theo định lí Viète, ta có: \({x_1} + {x_2} = - \frac{{11}}{2};{x_1}{x_2} = \frac{7}{2}\).
2. Áp dụng định lí Viète để tính nhẩm nghiệm
Giải phương trình bậc hai khi biết một nghiệm của nó
Xét phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). - Nếu \(a + b + c = 0\) thì phương trình có một nghiệm là \({x_1} = 1\), còn nghiệm kia là \({x_2} = \frac{c}{a}\). - Nếu \(a - b + c = 0\) thì phương trình có nghiệm là \({x_1} = - 1\), còn nghiệm kia là \({x_2} = - \frac{c}{a}\). |
Ví dụ: Phương trình \({x^2} - 6x + 5 = 0\) có \(a + b + c = 1 + \left( { - 6} \right) + 5 = 0\) nên phương trình có hai nghiệm: \({x_1} = 1,{x_2} = 5\).
Phương trình \(5{x^2} + 14x + 9 = 0\) có \(a - b + c = 5 - 14 + 9 = 0\) nên phương trình có hai nghiệm: \({x_1} = - 1,{x_2} = - \frac{9}{5}\).
3. Tìm hai số khi biết tổng và tích của chúng
Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình bậc hai: \({x^2} - Sx + P = 0\). Điều kiện để có hai số đó là \({S^2} - 4P \ge 0\). |
Ví dụ: Hai số có tổng bằng 9, tích bằng 20 là nghiệm của phương trình \({x^2} + 9x + 20 = 0\).
Ta có: \(\Delta = {\left( { - 9} \right)^2} - 4.1.20 = 1,\sqrt \Delta = 1\).
Suy ra phương trình có hai nghiệm \({x_1} = \frac{{9 - 1}}{2} = 4;{x_2} = \frac{{9 + 1}}{2} = 5\).
Vậy hai số cần tìm là 4 và 5.
Định lí Viète là một công cụ mạnh mẽ trong việc nghiên cứu và giải quyết các bài toán liên quan đến phương trình bậc hai. Trong chương trình Toán 9 Kết nối tri thức, việc nắm vững định lí này là vô cùng quan trọng để đạt kết quả tốt trong các bài kiểm tra và thi cử.
Cho phương trình bậc hai ax2 + bx + c = 0 (với a ≠ 0). Gọi x1 và x2 là hai nghiệm của phương trình. Khi đó:
Đây là hai công thức cơ bản của Định lí Viète, giúp chúng ta liên hệ giữa các hệ số của phương trình bậc hai và các nghiệm của nó.
Định lí Viète có rất nhiều ứng dụng trong việc giải toán, đặc biệt là trong các bài toán sau:
Ví dụ 1: Cho phương trình x2 - 5x + 6 = 0. Hãy tìm tổng và tích của hai nghiệm.
Giải:
Ta có a = 1, b = -5, c = 6. Theo Định lí Viète:
Ví dụ 2: Cho phương trình 2x2 + 3x - 5 = 0 và biết một nghiệm là x1 = 1. Hãy tìm nghiệm còn lại.
Giải:
Ta có a = 2, b = 3, c = -5. Theo Định lí Viète:
x1 + x2 = -3/2
1 + x2 = -3/2
x2 = -3/2 - 1 = -5/2
Để củng cố kiến thức về Định lí Viète, bạn có thể thực hành giải các bài tập sau:
Khi áp dụng Định lí Viète, cần lưu ý:
Hy vọng rằng với những kiến thức và ví dụ minh họa trên, bạn đã hiểu rõ hơn về Lý thuyết Định lí Viète và ứng dụng của nó trong chương trình Toán 9 Kết nối tri thức. Chúc bạn học tập tốt!