Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 71, 72 sách giáo khoa Toán 9 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án đầy đủ, dễ hiểu, kèm theo các bước giải chi tiết, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
Sử dụng MTCT tính các ti số lượng giác và làm tròn kết quả đến chữ số thập phân thứ ba: a) (sin {40^0}54';) b) (cos {52^0}15';) c) (tan {69^0}36') d) (cot {25^0}18')
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 5 trang 72SGK Toán 9 Kết nối tri thức
Dùng MTCT, tìm các góc \(\alpha \) (làm tròn đến phút) , biết:
a) \(\sin \alpha = 0,3782;\)
b) \(\cos \alpha = 0,6251;\)
c) \(\tan \alpha = 2,154;\)
d) \(\cot \alpha = 3,253.\)
Phương pháp giải:
Để tìm góc \(\alpha \) khi biết \(\sin \alpha = 0,3782\) thì ta bấm MTCT:
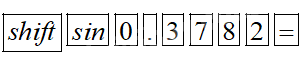
ta được kết quả 22,222231 thì ta bấm tiếp 0’’’ ta được kết quả \({22^0}13'20.03'' \approx {22^0}13'\) tương tự đối với trường hợp cos và tan. Tuy nhiên đối với trường hợp tìm \(\alpha \) khi biết \(\cot \alpha \) thì ta có thể tìm góc \({90^0} - \alpha \) (vì \(\tan \left( {{{90}^0} - \alpha } \right) = \cot \alpha \) từ đó ta tính được \(\alpha \)) .
Lời giải chi tiết:
a) \(\sin \alpha = 0,3782;\)
Ta có: \(\sin \alpha = 0,3782\) nên \(\alpha = {22^0}13'20,03'' \approx {22^0}13'\)
b) \(\cos \alpha = 0,6251;\)
Ta có: \(\cos \alpha = 0,6251\) nên \(\alpha = {51^0}18'37,7 \approx {51^0}19'\)
c) \(\tan \alpha = 2,154;\)
Ta có: \(\tan \alpha = 2,154\) nên \(\alpha = {65^0}5'48,46'' \approx {65^0}6'\)
d) \(\cot \alpha = 3,253.\)
Ta có: \(\cot \alpha = 3,253\) nên \({90^0} - \alpha = {72^0}54'43,65'' \approx {72^0}55'\)
Do đó \(\alpha \approx {90^0} - {72^0}55' = {17^0}5'\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 71 SGK Toán 9 Kết nối tri thức
Sử dụng MTCT tính các ti số lượng giác và làm tròn kết quả đến chữ số thập phân thứ ba:
a) \(\sin {40^0}54';\)
b) \(\cos {52^0}15';\)
c) \(\tan {69^0}36'\)
d) \(\cot {25^0}18'\)
Phương pháp giải:
Để tính \(\sin {40^0}54'\) ta bấm:
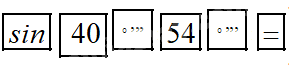
Tương tự với cos và tan.
Tuy nhiên đối với cot thì ta có thể làm như sau: \(\cot {25^0}18' = \frac{1}{{\tan {{25}^0}18'}}\) hoặc sử dụng tính chất hai góc phụ nhau có tan bằng cot.
Lời giải chi tiết:
a) \(\sin {40^0}54';\)
Ta có: \(\sin {40^0}54' = 0,6547408137 \approx 0,655\)
b) \(\cos {52^0}15';\)
Ta có: \(\cos {52^0}15' = 0,61221728 \approx 0,612\)
c) \(\tan {69^0}36'\)
Ta có: \(\tan {69^0}36' = 2,688918967 \approx 2,689\)
d) \(\cot {25^0}18'\)
Ta có: \(\tan {25^0}18' = 0,4726978344\) nên \(\cot {25^0}18' = \frac{1}{{\tan {{25}^0}18'}} = 2,115516356 \approx 2,116\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng trang 72 SGK Toán 9 Kết nối tri thức
Trở lại bài toán ở tình huống mở đầu: Trong một toàn chung cư, biết đoạn dốc vào sảnh toàn nhà dài 4 m, độ cao của đỉnh dốc bằng 0,4 m.
a) Hãy tính góc dốc.
b) Hỏi góc đó có đúng tiêu chuẩn của dốc cho người đi xe lăn không?
Tình huống mở đầu:
Ta có thể xác định “góc dốc” \(\alpha \) của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang là h không? (H.4.1)
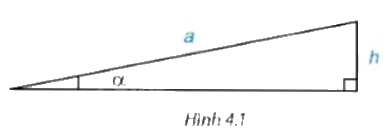
(Trong các tòa chung cư, người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc dốc bé hơn \({6^0}\)) .
Phương pháp giải:
Với con dốc ta biết chiều cao (cạnh đối) và chiều dài sảnh dốc (cạnh huyền) của tam giác vuông có góc nhọn \(\alpha \), để tính \(\alpha \) thì ta dùng tỉ số lượng giác \(\sin \alpha \)
Lời giải chi tiết:
a) Ta có: \(\sin \alpha = \frac{h}{a} = \frac{{0,4}}{4} = 0,1\), do đó \(\alpha \approx {5^0}44'.\)
b) \(\alpha \approx {5^0}44' < 6^0\)
Vậy góc đó đúng tiêu chuẩn cho người đi xe lăn.
Video hướng dẫn giải
Trả lời câu hỏi Tranh luận trang 72 SGK Toán 9 Kết nối tri thức
Để tính khoảng cách giữa hai địa điểm A, B không đo trực tiếp được, chẳng hạn A và B là hai địa điểm ở hai bên sông, người ta lấy điểm C về phía bờ sông có chứa B sao cho tam giác ABC vuông tại B. Ở bên bờ sông chứa B, người ta đo được \(\widehat {ACB} = \alpha \) và \(BC = a\) (H.4.10) . Với các dữ liệu đó, đã tính được khoảng cách AB chưa? Nếu được, hãy tính AB, biết \(\alpha = {55^0},a = 70\) m.
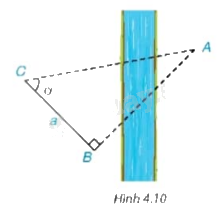
Phương pháp giải:
Tam giác ABC vuông tại B biết số đo góc \(\alpha \) và cạnh kề BC, cần tính cạnh AB (cạnh đối) do đó ta dùng tỉ số lượng giác \(\tan \alpha \)
Lời giải chi tiết:
Ta có: \(\tan \alpha = \frac{{AB}}{{BC}}\) hay \(\tan {55^0} = \frac{{AB}}{{70}}\) suy ra \(AB = 70.\tan {55^0} \approx 99,97\) m.
Vậy khoảng cách AB khoảng 99,97 m.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 71 SGK Toán 9 Kết nối tri thức
Sử dụng MTCT tính các ti số lượng giác và làm tròn kết quả đến chữ số thập phân thứ ba:
a) \(\sin {40^0}54';\)
b) \(\cos {52^0}15';\)
c) \(\tan {69^0}36'\)
d) \(\cot {25^0}18'\)
Phương pháp giải:
Để tính \(\sin {40^0}54'\) ta bấm:
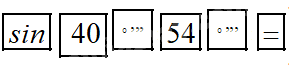
Tương tự với cos và tan.
Tuy nhiên đối với cot thì ta có thể làm như sau: \(\cot {25^0}18' = \frac{1}{{\tan {{25}^0}18'}}\) hoặc sử dụng tính chất hai góc phụ nhau có tan bằng cot.
Lời giải chi tiết:
a) \(\sin {40^0}54';\)
Ta có: \(\sin {40^0}54' = 0,6547408137 \approx 0,655\)
b) \(\cos {52^0}15';\)
Ta có: \(\cos {52^0}15' = 0,61221728 \approx 0,612\)
c) \(\tan {69^0}36'\)
Ta có: \(\tan {69^0}36' = 2,688918967 \approx 2,689\)
d) \(\cot {25^0}18'\)
Ta có: \(\tan {25^0}18' = 0,4726978344\) nên \(\cot {25^0}18' = \frac{1}{{\tan {{25}^0}18'}} = 2,115516356 \approx 2,116\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 5 trang 72SGK Toán 9 Kết nối tri thức
Dùng MTCT, tìm các góc \(\alpha \) (làm tròn đến phút) , biết:
a) \(\sin \alpha = 0,3782;\)
b) \(\cos \alpha = 0,6251;\)
c) \(\tan \alpha = 2,154;\)
d) \(\cot \alpha = 3,253.\)
Phương pháp giải:
Để tìm góc \(\alpha \) khi biết \(\sin \alpha = 0,3782\) thì ta bấm MTCT:
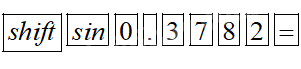
ta được kết quả 22,222231 thì ta bấm tiếp 0’’’ ta được kết quả \({22^0}13'20.03'' \approx {22^0}13'\) tương tự đối với trường hợp cos và tan. Tuy nhiên đối với trường hợp tìm \(\alpha \) khi biết \(\cot \alpha \) thì ta có thể tìm góc \({90^0} - \alpha \) (vì \(\tan \left( {{{90}^0} - \alpha } \right) = \cot \alpha \) từ đó ta tính được \(\alpha \)) .
Lời giải chi tiết:
a) \(\sin \alpha = 0,3782;\)
Ta có: \(\sin \alpha = 0,3782\) nên \(\alpha = {22^0}13'20,03'' \approx {22^0}13'\)
b) \(\cos \alpha = 0,6251;\)
Ta có: \(\cos \alpha = 0,6251\) nên \(\alpha = {51^0}18'37,7 \approx {51^0}19'\)
c) \(\tan \alpha = 2,154;\)
Ta có: \(\tan \alpha = 2,154\) nên \(\alpha = {65^0}5'48,46'' \approx {65^0}6'\)
d) \(\cot \alpha = 3,253.\)
Ta có: \(\cot \alpha = 3,253\) nên \({90^0} - \alpha = {72^0}54'43,65'' \approx {72^0}55'\)
Do đó \(\alpha \approx {90^0} - {72^0}55' = {17^0}5'\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng trang 72 SGK Toán 9 Kết nối tri thức
Trở lại bài toán ở tình huống mở đầu: Trong một toàn chung cư, biết đoạn dốc vào sảnh toàn nhà dài 4 m, độ cao của đỉnh dốc bằng 0,4 m.
a) Hãy tính góc dốc.
b) Hỏi góc đó có đúng tiêu chuẩn của dốc cho người đi xe lăn không?
Tình huống mở đầu:
Ta có thể xác định “góc dốc” \(\alpha \) của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang là h không? (H.4.1)
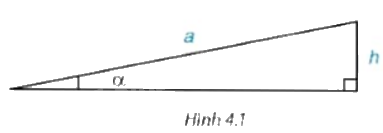
(Trong các tòa chung cư, người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc dốc bé hơn \({6^0}\)) .
Phương pháp giải:
Với con dốc ta biết chiều cao (cạnh đối) và chiều dài sảnh dốc (cạnh huyền) của tam giác vuông có góc nhọn \(\alpha \), để tính \(\alpha \) thì ta dùng tỉ số lượng giác \(\sin \alpha \)
Lời giải chi tiết:
a) Ta có: \(\sin \alpha = \frac{h}{a} = \frac{{0,4}}{4} = 0,1\), do đó \(\alpha \approx {5^0}44'.\)
b) \(\alpha \approx {5^0}44' < 6^0\)
Vậy góc đó đúng tiêu chuẩn cho người đi xe lăn.
Video hướng dẫn giải
Trả lời câu hỏi Tranh luận trang 72 SGK Toán 9 Kết nối tri thức
Để tính khoảng cách giữa hai địa điểm A, B không đo trực tiếp được, chẳng hạn A và B là hai địa điểm ở hai bên sông, người ta lấy điểm C về phía bờ sông có chứa B sao cho tam giác ABC vuông tại B. Ở bên bờ sông chứa B, người ta đo được \(\widehat {ACB} = \alpha \) và \(BC = a\) (H.4.10) . Với các dữ liệu đó, đã tính được khoảng cách AB chưa? Nếu được, hãy tính AB, biết \(\alpha = {55^0},a = 70\) m.
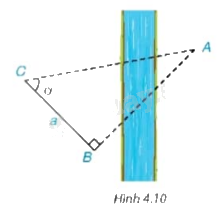
Phương pháp giải:
Tam giác ABC vuông tại B biết số đo góc \(\alpha \) và cạnh kề BC, cần tính cạnh AB (cạnh đối) do đó ta dùng tỉ số lượng giác \(\tan \alpha \)
Lời giải chi tiết:
Ta có: \(\tan \alpha = \frac{{AB}}{{BC}}\) hay \(\tan {55^0} = \frac{{AB}}{{70}}\) suy ra \(AB = 70.\tan {55^0} \approx 99,97\) m.
Vậy khoảng cách AB khoảng 99,97 m.
Mục 3 trang 71, 72 SGK Toán 9 tập 1 - Kết nối tri thức thường xoay quanh các chủ đề về hàm số bậc nhất, bao gồm việc xác định hàm số, vẽ đồ thị hàm số, và ứng dụng của hàm số trong giải quyết các bài toán thực tế. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản về hàm số, đặc biệt là hàm số bậc nhất.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0. 'a' được gọi là hệ số góc, quyết định độ dốc của đường thẳng biểu diễn hàm số. 'b' là tung độ gốc, là giao điểm của đường thẳng với trục Oy.
Để xác định một hàm số bậc nhất, cần biết giá trị của 'a' và 'b'. Ví dụ, hàm số y = 2x + 1 là một hàm số bậc nhất với a = 2 và b = 1.
Đồ thị của hàm số bậc nhất y = ax + b là một đường thẳng. Để vẽ đồ thị, ta thực hiện các bước sau:
Ví dụ, để vẽ đồ thị hàm số y = 2x + 1, ta có thể chọn x = 0, suy ra y = 1. Vậy điểm (0, 1) thuộc đồ thị. Chọn x = 1, suy ra y = 3. Vậy điểm (1, 3) thuộc đồ thị. Vẽ đường thẳng đi qua hai điểm (0, 1) và (1, 3).
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Để giải các bài toán ứng dụng, ta cần xác định được mối quan hệ giữa các đại lượng và biểu diễn mối quan hệ đó bằng một hàm số bậc nhất.
Bài tập 1: Cho hàm số y = -3x + 2. Tìm x khi y = 5.
Lời giải: Thay y = 5 vào hàm số, ta có: 5 = -3x + 2. Suy ra -3x = 3, do đó x = -1.
Bài tập 2: Vẽ đồ thị hàm số y = x - 1.
Lời giải: Chọn x = 0, suy ra y = -1. Vậy điểm (0, -1) thuộc đồ thị. Chọn x = 1, suy ra y = 0. Vậy điểm (1, 0) thuộc đồ thị. Vẽ đường thẳng đi qua hai điểm (0, -1) và (1, 0).
Các bài tập về hàm số bậc nhất thường gặp các dạng sau:
Để giải các bài tập này, cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, biết cách vẽ đồ thị hàm số và áp dụng các công thức liên quan.
Để củng cố kiến thức về hàm số bậc nhất, học sinh nên làm thêm nhiều bài tập khác nhau. Có thể tìm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online.
Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng, phong phú, giúp học sinh luyện tập và nâng cao kỹ năng giải toán. Chúng tôi hy vọng rằng bài viết này sẽ giúp các em học sinh hiểu rõ hơn về hàm số bậc nhất và tự tin giải các bài tập trong SGK Toán 9 tập 1 - Kết nối tri thức.
Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng cho việc học các kiến thức toán học nâng cao hơn trong các lớp học tiếp theo. Hãy dành thời gian ôn tập và luyện tập thường xuyên để đạt kết quả tốt nhất.