Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 89, 90 sách giáo khoa Toán 9 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án đầy đủ, kèm theo các bước giải chi tiết, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
Tại sao số đo cung lớn của một đường tròn luôn lớn hơn ({180^0})
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 89 SGK Toán 9 Kết nối tri thức
Tại sao số đo cung lớn của một đường tròn luôn lớn hơn \({180^0}\)
Phương pháp giải:
Dựa vào tổng số đo của cung nhỏ và cung lớn trên cùng một đường tròn bằng 360 độ.
Lời giải chi tiết:
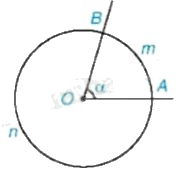
Xét đường tròn tâm O có cung AB nhỏ và cung AB lớn nên ta có
Sđ \(\overset\frown{AB}\) nhỏ + sđ \(\overset\frown{AB}\) lớn \(={{360}^{0}}\)
Và sđ \(\overset\frown{AB}\) lớn > sđ \(\overset\frown{AB}\) nhỏ
Nên sđ \(\overset\frown{AB}\) lớn + sđ \(\overset\frown{AB}\) lớn > sđ \(\overset\frown{AB}\) nhỏ + sđ \(\overset\frown{AB}\) lớn
2 . sđ \(\overset\frown{AB}\) lớn > \({{360}^{0}}\)
sđ \(\overset\frown{AB}\) lớn > \({{180}^{0}}\)
Nên số đo cung lớn luôn lớn hơn 180 độ.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 90 SGK Toán 9 Kết nối tri thức
Cho điểm C nằm trên đường tròn (O). Đường trung trực của đoạn OC cắt (O) tại A. Tính số đo của các cung \(\overset\frown{ACB}\) và \(\overset\frown{ABC}\).
Phương pháp giải:
- Tính số đo các góc OCA và OCB, từ đó suy ra số đo cung \(\overset\frown{AC}\), \(\overset\frown{BC}\) và \(\overset\frown{ACB}\).
-\(\overset\frown{ABC}\) là cung lớn có chung hai mút A, C với cung nhỏ \(\overset\frown{AC}\) nên sđ \(\overset\frown{ABC}=360{}^\circ -\) sđ\(\overset\frown{AC}\)
Lời giải chi tiết:
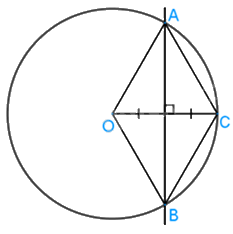
AB là đường trung trực của AB của OC nên AC = OA (tính chất đường trung trực)
mà OA = OC = R nên AC = OA = OC
hay \(\Delta \,ACO\) là tam giác đều.
Do đó: \(\widehat{AOC}=60{}^\circ \) (tính chất của tam giác đều) \(\Rightarrow \) sđ \(\overset\frown{AC}=60{}^\circ \)
Tương tự ta có: sđ \(\overset\frown{BC}=60{}^\circ \)
Suy ra:
sđ \(\overset\frown{ACB}=\)sđ \(\overset\frown{AC}\) + sđ \(\overset\frown{BC}=60{}^\circ +60{}^\circ =120{}^\circ \)
\(\overset\frown{ABC}\) là cung lớn có chung hai mút A, C với cung nhỏ \(\overset\frown{AC}\)
nên sđ \(\overset\frown{ABC}=360{}^\circ -\) sđ\(\overset\frown{AC}=360{}^\circ -60{}^\circ =300{}^\circ \)
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 89 SGK Toán 9 Kết nối tri thức
Tại sao số đo cung lớn của một đường tròn luôn lớn hơn \({180^0}\)
Phương pháp giải:
Dựa vào tổng số đo của cung nhỏ và cung lớn trên cùng một đường tròn bằng 360 độ.
Lời giải chi tiết:
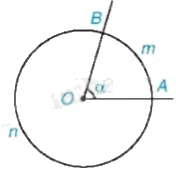
Xét đường tròn tâm O có cung AB nhỏ và cung AB lớn nên ta có
Sđ \(\overset\frown{AB}\) nhỏ + sđ \(\overset\frown{AB}\) lớn \(={{360}^{0}}\)
Và sđ \(\overset\frown{AB}\) lớn > sđ \(\overset\frown{AB}\) nhỏ
Nên sđ \(\overset\frown{AB}\) lớn + sđ \(\overset\frown{AB}\) lớn > sđ \(\overset\frown{AB}\) nhỏ + sđ \(\overset\frown{AB}\) lớn
2 . sđ \(\overset\frown{AB}\) lớn > \({{360}^{0}}\)
sđ \(\overset\frown{AB}\) lớn > \({{180}^{0}}\)
Nên số đo cung lớn luôn lớn hơn 180 độ.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 90 SGK Toán 9 Kết nối tri thức
Cho điểm C nằm trên đường tròn (O). Đường trung trực của đoạn OC cắt (O) tại A. Tính số đo của các cung \(\overset\frown{ACB}\) và \(\overset\frown{ABC}\).
Phương pháp giải:
- Tính số đo các góc OCA và OCB, từ đó suy ra số đo cung \(\overset\frown{AC}\), \(\overset\frown{BC}\) và \(\overset\frown{ACB}\).
-\(\overset\frown{ABC}\) là cung lớn có chung hai mút A, C với cung nhỏ \(\overset\frown{AC}\) nên sđ \(\overset\frown{ABC}=360{}^\circ -\) sđ\(\overset\frown{AC}\)
Lời giải chi tiết:
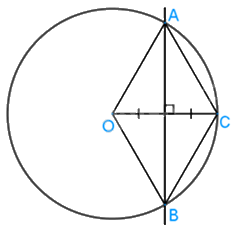
AB là đường trung trực của AB của OC nên AC = OA (tính chất đường trung trực)
mà OA = OC = R nên AC = OA = OC
hay \(\Delta \,ACO\) là tam giác đều.
Do đó: \(\widehat{AOC}=60{}^\circ \) (tính chất của tam giác đều) \(\Rightarrow \) sđ \(\overset\frown{AC}=60{}^\circ \)
Tương tự ta có: sđ \(\overset\frown{BC}=60{}^\circ \)
Suy ra:
sđ \(\overset\frown{ACB}=\)sđ \(\overset\frown{AC}\) + sđ \(\overset\frown{BC}=60{}^\circ +60{}^\circ =120{}^\circ \)
\(\overset\frown{ABC}\) là cung lớn có chung hai mút A, C với cung nhỏ \(\overset\frown{AC}\)
nên sđ \(\overset\frown{ABC}=360{}^\circ -\) sđ\(\overset\frown{AC}=360{}^\circ -60{}^\circ =300{}^\circ \)
Mục 2 trang 89, 90 SGK Toán 9 tập 1 - Kết nối tri thức tập trung vào việc ôn tập chương 1: Số thực. Đây là một phần quan trọng giúp học sinh củng cố kiến thức về số thực, các phép toán trên số thực, và ứng dụng của số thực trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức này là nền tảng cho các chương học tiếp theo.
Mục 2 bao gồm các bài tập vận dụng các kiến thức đã học về:
Bài tập 1 yêu cầu học sinh xác định các số thực thuộc tập hợp số nào (số hữu tỉ, số vô tỉ, số thực). Để giải bài tập này, học sinh cần nắm vững định nghĩa của từng loại số:
Ví dụ: Số 2,5 là số hữu tỉ vì có thể viết dưới dạng 5/2. Số π là số vô tỉ vì không thể viết dưới dạng phân số. Số -3 là số hữu tỉ vì có thể viết dưới dạng -3/1.
Bài tập 2 yêu cầu học sinh so sánh các số thực. Để so sánh các số thực, học sinh có thể sử dụng các phương pháp sau:
Ví dụ: Để so sánh 2√3 và 3√2, ta bình phương hai vế: (2√3)² = 12 và (3√2)² = 18. Vì 12 < 18, nên 2√3 < 3√2.
Bài tập 3 yêu cầu học sinh thực hiện các phép toán trên số thực. Để giải bài tập này, học sinh cần nắm vững các quy tắc về phép cộng, trừ, nhân, chia số thực.
Ví dụ: (2 + √3) + (1 - √3) = 2 + 1 + √3 - √3 = 3.
Kiến thức về số thực là nền tảng cho nhiều chương học tiếp theo trong chương trình Toán 9, cũng như các môn học khác. Việc nắm vững kiến thức này sẽ giúp học sinh tự tin hơn trong học tập và giải quyết các bài toán thực tế.
Giaitoan.edu.vn là website học Toán 9 online uy tín, cung cấp đầy đủ các bài giải SGK Toán 9 tập 1, tập 2, các bài tập trắc nghiệm, và các tài liệu học tập hữu ích khác. Chúng tôi luôn cập nhật nội dung mới nhất và đảm bảo tính chính xác của các bài giải. Hãy truy cập Giaitoan.edu.vn để học Toán 9 hiệu quả hơn!