Bài tập 6.16 trang 19 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 6.16 trang 19 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Biết rằng parabol (y = a{x^2}left( {a ne 0} right)) đi qua điểm (Aleft( {2;4sqrt 3 } right)). a) Tìm hệ số a và vẽ đồ thị của hàm số (y = a{x^2}) với a vừa tìm được. b) Tìm tung độ của điểm thuộc parabol có hoành độ (x = - 1). c) Tìm các điểm thuộc parabol có tung độ (y = 5sqrt 3 ).
Đề bài
Biết rằng parabol \(y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {2;4\sqrt 3 } \right)\).
a) Tìm hệ số a và vẽ đồ thị của hàm số \(y = a{x^2}\) với a vừa tìm được.
b) Tìm tung độ của điểm thuộc parabol có hoành độ \(x = - 1\).
c) Tìm các điểm thuộc parabol có tung độ \(y = 5\sqrt 3 \).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Thay \(x = 2;y = 4\sqrt 3 \) vào hàm số \(y = a{x^2}\), giải phương trình thu được tìm được a.
+ Thay a vừa tìm được để viết parabol \(y = a{x^2}\).
+ Cách vẽ parabol \(y = a{x^2}\left( {a \ne 0} \right)\)
- Lập bảng ghi một số cặp giá trị tương ứng của x và y.
- Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
b) Thay \(x = - 1\) vào parabol tìm được trong câu a để tìm tung độ.
c) Thay \(y = 5\sqrt 3 \) vào parabol tìm được trong câu a để tìm hoành độ.
Lời giải chi tiết
a) Vì parabol \(y = a{x^2}\) đi qua điểm \(A\left( {2;4\sqrt 3 } \right)\) nên ta có: \(4\sqrt 3 = a{.2^2} \Rightarrow a = \sqrt 3 \)
Suy ra, parabol cần tìm là: \(y = \sqrt 3 {x^2}\).
Vẽ đồ thị hàm số \(y = \sqrt 3 {x^2}\):
Lập bảng một số cặp giá trị tương ứng của x và y:

Biểu diễn các điểm \(\left( { - 2;4\sqrt 3 } \right);\left( { - 1;\sqrt 3 } \right);\left( {0;0} \right);\left( {1;\sqrt 3 } \right);\left( {2;4\sqrt 3 } \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số \(y = \sqrt 3 {x^2}\) như hình vẽ.
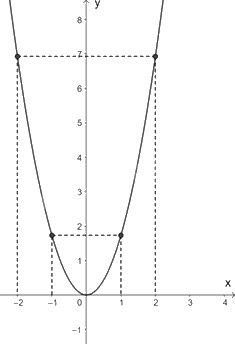
b) Thay \(x = - 1\) vào hàm số \(y = \sqrt 3 {x^2}\) ta có: \(y = \sqrt 3 .{\left( { - 1} \right)^2} = \sqrt 3 \). Vậy tung độ của điểm thuộc parabol có hoành độ \(x = - 1\) là \(y = \sqrt 3 \).
c) Thay \(y = 5\sqrt 3 \) vào hàm số \(y = \sqrt 3 {x^2}\) ta có: \(5\sqrt 3 = \sqrt 3 .{x^2}\), suy ra \(x = \sqrt 5 \) hoặc \(x = - \sqrt 5 \).
Vậy các điểm thuộc parabol có tung độ \(y = 5\sqrt 3 \) là \(\left( {\sqrt 5 ;5\sqrt 3 } \right);\left( { - \sqrt 5 ;5\sqrt 3 } \right)\).
Bài tập 6.16 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán thực tế, yêu cầu học sinh xây dựng và giải hệ phương trình bậc nhất hai ẩn. Để giải bài tập này, các em cần nắm vững các kiến thức sau:
Bài toán 6.16 SGK Toán 9 tập 2 thường mô tả một tình huống thực tế, trong đó có hai đại lượng liên quan đến nhau. Các em cần xác định hai đại lượng này và đặt ẩn cho chúng. Sau đó, dựa vào các thông tin được cung cấp trong bài toán, các em xây dựng hai phương trình để mô tả mối quan hệ giữa hai đại lượng này. Cuối cùng, các em giải hệ phương trình vừa xây dựng để tìm ra giá trị của các ẩn.
(Ở đây sẽ là lời giải chi tiết của bài tập 6.16, bao gồm các bước giải, giải thích rõ ràng và kết luận. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu tìm chiều dài và chiều rộng của một mảnh đất hình chữ nhật, biết rằng chu vi của mảnh đất là 50m và chiều dài hơn chiều rộng 5m.
Ngoài bài tập 6.16, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế. Để giải các bài tập này, các em cần:
Để củng cố kiến thức và kỹ năng giải bài tập về hệ phương trình bậc nhất hai ẩn, các em có thể luyện tập thêm các bài tập sau:
Bài tập 6.16 trang 19 SGK Toán 9 tập 2 - Kết nối tri thức là một bài tập quan trọng, giúp các em học sinh rèn luyện kỹ năng giải hệ phương trình bậc nhất hai ẩn và ứng dụng kiến thức vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin hơn trong việc học tập môn Toán.