Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, tập xác định và tập giá trị để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
Cho hàm số y = f(x) = 2sin2x
Chứng minh rằng với số nguyên \(k\) tùy ý, luôn có \(f(x + kπ) = f(x)\) với mọi \(x\).
Lời giải chi tiết:
Ta có \(f(x + kπ) = 2\sin 2(x + kπ) \)
\(= 2\sin (2x + k2π) = 2\sin 2x = f(x),\) \( ∀ x \in\mathbb R\)
Lập bảng biến thiên của hàm số \(y = 2\sin 2x\) trên đoạn \(\left[ { - {\pi \over 2};{\pi \over 2}} \right].\)
Lời giải chi tiết:
Bảng biến thiên :
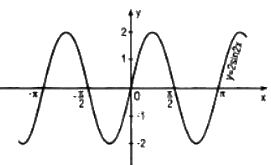
Vẽ đồ thị của hàm số \(y = 2\sin 2x\).
Lời giải chi tiết:
Đồ thị :

Câu 6 trang 15 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học kỳ I, tập trung vào việc củng cố kiến thức về hàm số, đặc biệt là các khái niệm về tập xác định, tập giá trị, và cách xác định hàm số thông qua các điều kiện cho trước. Bài tập này thường yêu cầu học sinh phải hiểu rõ định nghĩa của hàm số, các phép toán trên hàm số, và khả năng phân tích bài toán để tìm ra phương pháp giải phù hợp.
Thông thường, bài tập này sẽ đưa ra một hàm số cụ thể và yêu cầu học sinh:
Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các bước sau:
Giả sử hàm số được cho là: y = √(4 - x²)
Giải:
Ngoài Câu 6 trang 15, SGK Đại số và Giải tích 11 Nâng cao còn nhiều bài tập tương tự khác. Các bài tập này thường yêu cầu học sinh vận dụng các kiến thức về hàm số để giải quyết các bài toán thực tế. Để nâng cao khả năng giải toán, học sinh nên luyện tập thêm các bài tập khác trong sách giáo khoa và các tài liệu tham khảo. Việc hiểu rõ bản chất của các khái niệm và phương pháp giải là rất quan trọng để có thể áp dụng chúng vào các bài toán khác nhau.
Khi giải bài tập này, học sinh cần lưu ý:
Câu 6 trang 15 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số. Bằng cách nắm vững các phương pháp giải và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong học tập.