Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và ứng dụng vào hình học không gian.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho đường tròn
Đề bài
Cho đường tròn \((O; R)\) , đường thẳng \(△\) và điểm I . Tìm điểm A trên \((O; R)\) và điểm B trên \(△\) sao cho I là trung điểm của đoạn thẳng AB
Lời giải chi tiết
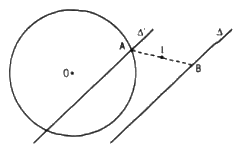
Giả sử ta đã có điểm A trên đường tròn \((O ; R)\) và điểm B trên △ sao cho I là trung điểm của đoạn thẳng AB
Phép đối xứng tâm ĐI biến điểm B thành điểm A nên biến đường thẳng \(△\) thành đường thẳng \(△’\) đi qua A.
Mặt khác A lại nằm trên \((O ; R)\) nên A phải là giao điểm của \(△’\) và \((O ; R)\)
Suy ra cách dựng:
Dựng đường thẳng \(△’\) là ảnh của \(△\) qua phép đối xứng tâm ĐI. Lấy A là giao điểm (nếu có) của \(△’\) và \((O ; R)\), còn B là giao điểm của đường thẳng AI và đường thẳng \(△\)
Bài 18 trang 19 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học không gian, cụ thể là phần vectơ trong không gian. Bài toán này thường kiểm tra khả năng vận dụng các định lý, tính chất về vectơ để giải quyết các bài toán liên quan đến hình học.
(Đề bài cụ thể sẽ được chèn vào đây - ví dụ: Cho hình hộp ABCD.A'B'C'D'. Gọi I là trung điểm của AB. Chứng minh rằng vectơ AI bằng một nửa vectơ AB.)
Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức sau:
Phương pháp giải thường được sử dụng là:
(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng và chính xác. Ví dụ:
Vì I là trung điểm của AB nên AI = IB. Do đó, vectơ AI = 1/2 vectơ AB.
Chứng minh: ...
Kết luận: ...
Để hiểu rõ hơn về cách giải bài toán này, chúng ta cùng xem xét một ví dụ minh họa:
(Ví dụ minh họa sẽ được trình bày ở đây, bao gồm đề bài, lời giải và giải thích.)
Dưới đây là một số bài tập tương tự để bạn luyện tập:
Khi giải các bài tập về vectơ trong không gian, bạn cần lưu ý những điều sau:
Câu 18 trang 19 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng vào hình học không gian. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, bạn đã nắm vững kiến thức và kỹ năng giải toán này. Hãy luyện tập thêm các bài tập tương tự để nâng cao khả năng của mình.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!