Câu 18 trang 226 SGK Đại số và Giải tích 11 Nâng cao

Câu 18 trang 226 SGK Đại số và Giải tích 11 Nâng cao: Phân tích chi tiết và lời giải

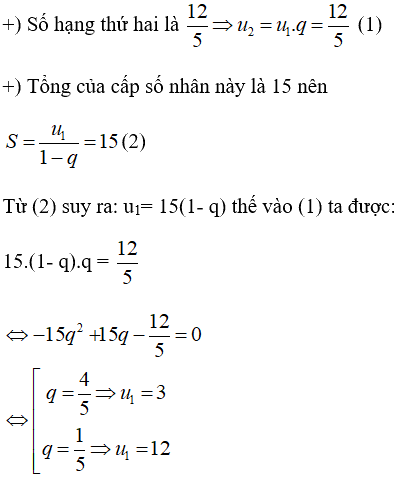
Bài tập Câu 18 trang 226 thuộc chương trình Đại số và Giải tích 11 Nâng cao, thường tập trung vào việc vận dụng các kiến thức đã học về hàm số, đạo hàm, giới hạn, hoặc các chủ đề khác tùy thuộc vào nội dung cụ thể của bài toán. Việc hiểu rõ bản chất của bài toán và áp dụng đúng các công thức, định lý là yếu tố then chốt để đạt được kết quả chính xác.

I. Đề bài Câu 18 trang 226 SGK Đại số và Giải tích 11 Nâng cao

(Nội dung đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho hàm số y = f(x) = x^3 - 3x^2 + 2. Tìm các điểm cực trị của hàm số.)

II. Phương pháp giải quyết

Để giải quyết bài toán này, chúng ta cần thực hiện các bước sau:

1. Xác định tập xác định của hàm số: Kiểm tra xem hàm số có tồn tại tại mọi điểm hay không.
2. Tính đạo hàm cấp một: Đạo hàm cấp một của hàm số sẽ giúp chúng ta tìm ra các điểm nghi ngờ là cực trị.
3. Tìm các điểm làm đạo hàm cấp một bằng 0 hoặc không xác định: Đây là các điểm mà tại đó hàm số có thể đạt cực trị.
4. Khảo sát dấu của đạo hàm cấp một: Sử dụng bảng xét dấu hoặc phương pháp khác để xác định xem hàm số tăng hay giảm trên các khoảng xác định.
5. Kết luận về cực trị: Dựa vào dấu của đạo hàm cấp một, chúng ta có thể kết luận về các điểm cực đại, cực tiểu của hàm số.

III. Lời giải chi tiết Câu 18 trang 226

(Lời giải chi tiết, từng bước, có giải thích rõ ràng sẽ được trình bày ở đây. Ví dụ:)

Bước 1: Tập xác định của hàm số y = f(x) = x^3 - 3x^2 + 2 là R (tập hợp tất cả các số thực).

Bước 2: Tính đạo hàm cấp một: f'(x) = 3x^2 - 6x.

Bước 3: Giải phương trình f'(x) = 0: 3x^2 - 6x = 0 => 3x(x - 2) = 0 => x = 0 hoặc x = 2.

Bước 4: Khảo sát dấu của đạo hàm cấp một:

Bước 5: Kết luận: Hàm số đạt cực đại tại x = 0, với giá trị f(0) = 2. Hàm số đạt cực tiểu tại x = 2, với giá trị f(2) = -2.

IV. Lưu ý khi giải Câu 18 trang 226 và các bài tập tương tự

• Nắm vững các định nghĩa và công thức: Đảm bảo bạn hiểu rõ các khái niệm về hàm số, đạo hàm, giới hạn, và các công thức liên quan.
• Thực hành thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập khác nhau.
• Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
• Sử dụng các công cụ hỗ trợ: Nếu cần thiết, bạn có thể sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán để kiểm tra kết quả hoặc tìm kiếm lời giải.

V. Mở rộng kiến thức

Ngoài việc giải Câu 18 trang 226, bạn nên tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, chẳng hạn như tìm cực trị của hàm số, xét tính đơn điệu của hàm số, hoặc tìm điểm uốn của đồ thị hàm số. Việc mở rộng kiến thức sẽ giúp bạn hiểu sâu hơn về môn toán và ứng dụng nó vào các lĩnh vực khác.

Hy vọng với lời giải chi tiết và những lưu ý trên, bạn đã hiểu rõ cách giải Câu 18 trang 226 SGK Đại số và Giải tích 11 Nâng cao. Chúc bạn học tốt!