Giải Câu 19 Trang 29 SGK Đại số và Giải tích 11 Nâng cao

Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao

Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học.

Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đồ thị hàm số và các phép biến đổi đồ thị để giải quyết.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.

a.Vẽ đồ thị của hàm số y = tanx rồi chỉ ra trên đồ thị đó có các điểm có hoành độ thuộc khoảng (-π ; π) là nghiệm của mỗi phương trình sau

LG a

Vẽ đồ thị của hàm số \(y = \tan x\) rồi chỉ ra trên đồ thị đó có các điểm có hoành độ thuộc khoảng \((-π ; π)\) là nghiệm của mỗi phương trình sau

1. \(\tan x = -1\)

2. \(\tan x = 0\)

Lời giải chi tiết:

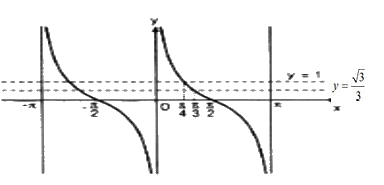
Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao 1

1. Phương trình \(\tan x = -1\) có nghiệm thuộc khoảng \((-π ; π)\) là :

\(x = - {\pi \over 4}\,\text{ và }\,x = {{3\pi } \over 4}\)

2. Phương trình \(\tan x = 0\) có nghiệm thuộc khoảng \((-π ; π)\) là \(x = 0\)

LG b

Cũng câu hỏi tương tự cho hàm số \(y = \cot x\) và cho mỗi phương trình sau

1. \(\cot x = {{\sqrt 3 } \over 3}\)

2. \(\cot x = 1\)

Lời giải chi tiết:

Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao 1

1. Phương trình có nghiệm thuộc khoảng \((-π ; π)\) là :

\(x = {\pi \over 3}\,\text{ và }\,x = - {{2\pi } \over 3}\)

2. Phương trình \(\cot x = 1\) có nghiệm thuộc khoảng \((-π ; π)\) là :

\(x = {\pi \over 4}\,\text{ và }\,x = - {{3\pi } \over 4}\)

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao – hành trang không thể thiếu trong chuyên mục toán 11 trên nền tảng soạn toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải Chi Tiết Câu 19 Trang 29 SGK Đại số và Giải tích 11 Nâng cao

Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học về hàm số bậc hai. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về:

Định nghĩa hàm số bậc hai.
Dạng tổng quát của hàm số bậc hai: y = ax² + bx + c (a ≠ 0).
Hệ số a, b, c và vai trò của chúng trong việc xác định tính chất của parabol.
Đỉnh của parabol: I(-b/2a, -Δ/4a).
Trục đối xứng của parabol: x = -b/2a.
Bảng biến thiên của hàm số bậc hai.

Phân Tích Đề Bài

Trước khi đi vào giải chi tiết, chúng ta cần phân tích kỹ đề bài để xác định yêu cầu và các dữ kiện đã cho. Thông thường, bài tập dạng này sẽ yêu cầu:

Xác định các hệ số a, b, c của hàm số.
Tìm tọa độ đỉnh của parabol.
Vẽ đồ thị hàm số.
Tìm các điểm mà đồ thị hàm số đi qua.
Giải các bài toán liên quan đến ứng dụng của hàm số bậc hai.

Lời Giải Chi Tiết

Để minh họa, giả sử đề bài yêu cầu giải hàm số y = x² - 4x + 3.

Xác định hệ số: a = 1, b = -4, c = 3.
Tìm tọa độ đỉnh:
- x_I = -b/2a = -(-4)/(2*1) = 2.
- y_I = -Δ/4a = -((-4)² - 4*1*3)/(4*1) = -(16 - 12)/4 = -1.
Vậy, tọa độ đỉnh của parabol là I(2, -1).
Tìm trục đối xứng: x = 2.
Vẽ đồ thị:
- Xác định một vài điểm thuộc đồ thị, ví dụ:
  - Khi x = 0, y = 3.
  - Khi x = 1, y = 0.
  - Khi x = 3, y = 0.
  - Khi x = 4, y = 3.
- Vẽ parabol đi qua các điểm đã xác định và có đỉnh I(2, -1).

Các Dạng Bài Tập Liên Quan

Ngoài việc giải trực tiếp hàm số, học sinh có thể gặp các dạng bài tập liên quan như:

Tìm điều kiện để hàm số có cực trị: Δ > 0.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: Dựa vào tọa độ đỉnh và hệ số a.
Giải phương trình, bất phương trình bậc hai: Sử dụng đồ thị hàm số hoặc công thức nghiệm.
Ứng dụng hàm số bậc hai vào các bài toán thực tế: Ví dụ, bài toán tìm quỹ đạo của vật thể chuyển động.

Mẹo Giải Bài Tập

Để giải các bài tập về hàm số bậc hai một cách hiệu quả, bạn nên:

Nắm vững các kiến thức cơ bản về hàm số bậc hai.
Luyện tập thường xuyên với nhiều dạng bài tập khác nhau.
Sử dụng đồ thị hàm số để trực quan hóa bài toán.
Kiểm tra lại kết quả sau khi giải xong.

Kết Luận

Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Bằng cách nắm vững các kiến thức cơ bản và luyện tập thường xuyên, bạn có thể tự tin giải quyết mọi bài tập liên quan đến chủ đề này.

Hy vọng với lời giải chi tiết và các hướng dẫn trên, bạn đã hiểu rõ cách giải Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao. Chúc bạn học tập tốt!