Bài toán này thường yêu cầu học sinh vận dụng các kiến thức về hàm số, đạo hàm, hoặc các chủ đề khác đã được học để tìm ra lời giải chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
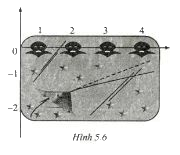
Hình 5.6 thể hiện màn hình của một trò chơi
Đề bài
Hình 5.6 thể hiện màn hình của một trò chơi điện tử. Một máy bay xuất hiện ở bên trái màn hình rồi bay sang phải theo một quỹ đạo (C) là đồ thị của hàm số \(y = f\left( x \right)\) , trong đó \(f\left( x \right) = - 1 - {1 \over x},\left( {x > 0} \right).\) Biết rằng tên lửa được bắn ra từ máy bay tại một điểm thuộc (C) sẽ bay theo phương tiếp tuyến của (C) tại điểm đó. Tìm hoành độ các điểm thuộc (C) sao cho tên lửa bắn ra từ đó có thể bắn trúng một trong bốn mục tiêu nằm ở trên màn hình có tọa độ (1 ; 0), (2 ; 0), (3 ; 0) và (4 ; 0) (làm tròn kết quả đến hàng phần vạn)
Lời giải chi tiết
Ta có: \(f'\left( x \right) = {1 \over {{x^2}}}\)
Phương trình tiếp tuyến (d) của quỹ đạo (C) tại tiếp điểm \({M_0}\left( {{x_0}; - 1 - {1 \over {{x_0}}}} \right)\) là :
\(\eqalign{ & y = {1 \over {x_0^2}}\left( {x - {x_0}} \right) - 1 - {1 \over {{x_0}}} \cr & hay\,x_0^2 + 2{x_0} - x + x_0^2y = 0 \cr} \)
Ta phải tìm x0 > 0, sao cho (d) lần lượt đi qua 4 điểm có tọa độ (1 ; 0), (2 ; 0), (3 ; 0) và (4 ; 0).
a. Với x = 1, y = 0, ta có \(x_0^2 + 2{x_0} - 1 = 0.\)
Suy ra \({x_0} = - 1 + \sqrt 2 \approx 0,4142\)
b. Với x = 2, y = 0, ta có \(x_0^2 + 2{x_0} - 2 = 0.\)
Suy ra \({x_0} = - 1 + \sqrt 3 \approx 0,7321\)
c. Với x = 3, y = 0, ta có \(x_0^2 + 2{x_0} - 3 = 0.\)
Suy ra \({x_0} = 1\)
d. Với x = 4, y = 0, ta có \(x_0^2 + 2{x_0} - 4 = 0.\)
Suy ra \({x_0} = - 1 + \sqrt 5 \approx 1,2361\)
Bài toán Câu 26 trang 205 trong sách giáo khoa Đại số và Giải tích 11 Nâng cao thường là một bài tập ứng dụng cao, đòi hỏi học sinh phải nắm vững kiến thức nền tảng và kỹ năng giải quyết vấn đề. Bài viết này sẽ cung cấp một phân tích chi tiết về bài toán, các bước giải cụ thể, và những lưu ý quan trọng để giúp bạn hiểu rõ và tự tin giải quyết bài toán này.
Trước khi đi vào lời giải, chúng ta cần hiểu rõ đề bài. Thông thường, bài toán Câu 26 trang 205 sẽ liên quan đến một trong các chủ đề sau:
Việc phân tích kỹ đề bài sẽ giúp bạn xác định được phương pháp giải phù hợp và tránh những sai sót không đáng có.
Để minh họa, chúng ta sẽ giả sử bài toán Câu 26 trang 205 là một bài toán về tìm cực trị của hàm số. Giả sử hàm số được cho là:
f(x) = x3 - 3x2 + 2
f'(x) = 3x2 - 6x
Giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, các điểm dừng là x = 0 và x = 2.
f''(x) = 6x - 6
Tại x = 0:
f''(0) = -6 < 0 => Hàm số đạt cực đại tại x = 0.
Giá trị cực đại là f(0) = 2.
Tại x = 2:
f''(2) = 6 > 0 => Hàm số đạt cực tiểu tại x = 2.
Giá trị cực tiểu là f(2) = -2.
Vậy, hàm số f(x) = x3 - 3x2 + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Khi giải các bài toán về hàm số, đạo hàm, hoặc giới hạn, bạn cần lưu ý những điều sau:
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau:
Bài toán Câu 26 trang 205 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp bạn rèn luyện kỹ năng giải toán và củng cố kiến thức về các chủ đề liên quan. Hy vọng rằng, với những phân tích chi tiết và lời giải cụ thể trong bài viết này, bạn sẽ tự tin hơn khi đối mặt với bài toán này và các bài toán tương tự.