Bài tập Câu 4 trang 223 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài toán này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.
Giải các phương trình :
\({\sin ^4}x + {\cos ^4}x = {3 \over 4}\)
Lời giải chi tiết:
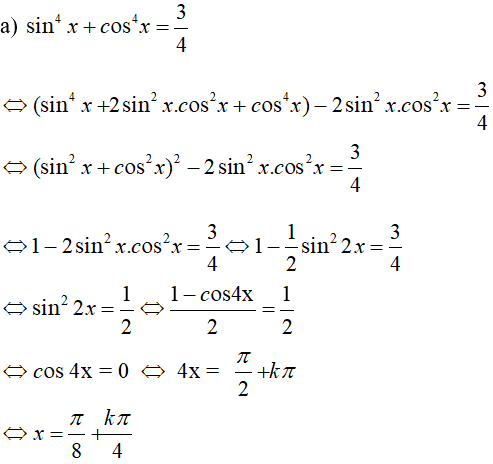
\({\sin ^2}2x - {\sin ^2}x = {\sin ^2}{\pi \over 4}\)
Lời giải chi tiết:
\(\eqalign{ & {\sin ^2}2x - {\sin ^2}x = {\sin ^2}{\pi \over 4} \cr & \Leftrightarrow 4{\sin ^2}x{\cos ^2}x - {\sin ^2}x = {1 \over 2} \cr & \Leftrightarrow 8{\sin ^2}x\left( {1 - {{\sin }^2}x} \right) - 2{\sin ^2}x = 1 \cr & \Leftrightarrow 8{\sin ^4}x - 6{\sin ^2}x + 1 = 0 \cr & \Leftrightarrow \left[ {\matrix{ {{{\sin }^2}x = {1 \over 2}} \cr {{{\sin }^2}x = {1 \over 4}} \cr } } \right. \Leftrightarrow \left[ {\matrix{ {{{1 - \cos 2x} \over 2} = {1 \over 2}} \cr {{{1 - \cos 2x} \over 2} = {1 \over 4}} \cr } } \right. \cr & \Leftrightarrow \left[ {\matrix{ {\cos 2x = 0} \cr {\cos 2x = {1 \over 2}} \cr } } \right. \cr} \)
\( \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{2} + k\pi \\2x = \pm \frac{\pi }{3} + k2\pi \end{array} \right. \) \(\Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + \frac{{k\pi }}{2}\\x = \pm \frac{\pi }{6} + k\pi \end{array} \right.\)
\(\cos x\cos 2x = \cos 3x\)
Lời giải chi tiết:
\(\eqalign{ & \cos x\cos 2x = \cos 3x \cr & \Leftrightarrow {1 \over 2}\left( {\cos 3x + \cos x} \right) = \cos 3x \cr & \Leftrightarrow \cos 3x = \cos x \cr & \Leftrightarrow \left[ {\matrix{ {3x = x + k2\pi } \cr {3x = - x + k2\pi } \cr } } \right. \Leftrightarrow \left[ {\matrix{ {x = k\pi } \cr {x = k{\pi \over 2}} \cr } } \right.\cr& \Leftrightarrow x = k{\pi \over 2},k \in\mathbb Z \cr} \)
\(\tan 2x - \sin 2x + \cos 2x - 1 = 0\)
Lời giải chi tiết:
Điều kiện: \(\cos 2x \ne0\)
Ta có: \(\tan 2x = \dfrac{{\sin 2x}}{{\cos 2x}} \) \(\Rightarrow \sin 2x = \tan 2x\cos 2x\)
\(\eqalign{ & \tan 2x - \sin 2x + \cos 2x - 1 = 0 \cr & \Leftrightarrow \tan 2x - \tan 2x\cos 2x + \cos 2x - 1 = 0\cr & \Leftrightarrow \tan 2x\left( {1 - \cos 2x} \right) - \left( {1 - \cos 2x} \right) = 0 \cr & \Leftrightarrow \left( {1 - \cos 2x} \right)\left( {\tan 2x - 1} \right) = 0 \cr & \Leftrightarrow \left[ {\matrix{ {\tan 2x = 1} \cr {\cos 2x = 1} \cr } } \right. \cr} \)
\( \Leftrightarrow \left[ \begin{array}{l}2x = \dfrac{\pi }{4} + k\pi \\2x = k2\pi \end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{2}\\x = k\pi \end{array} \right.,k \in Z\)
Bài tập Câu 4 trang 223 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học lớp 11, tập trung vào việc ứng dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng phân tích chi tiết từng bước.
Trước khi đi vào giải bài, điều quan trọng là phải hiểu rõ yêu cầu của đề bài. Thông thường, các bài tập liên quan đến đạo hàm sẽ yêu cầu chúng ta tính đạo hàm của một hàm số, tìm cực trị, hoặc giải các phương trình, bất phương trình chứa đạo hàm. Câu 4 trang 223 thường tập trung vào việc tìm khoảng đơn điệu của hàm số.
Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức sau:
Giả sử đề bài yêu cầu tìm khoảng đơn điệu của hàm số f(x) = x3 - 3x2 + 2.
f'(x) = 3x2 - 6x
Giải phương trình f'(x) = 0 để tìm các điểm cực trị:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Hàm số f(x) đồng biến trên các khoảng (-∞; 0) và (2; +∞). Hàm số f(x) nghịch biến trên khoảng (0; 2).
Ngoài bài tập Câu 4 trang 223, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết. Một số dạng bài tập phổ biến bao gồm:
Để giải các bài tập về đạo hàm một cách hiệu quả, học sinh nên:
Đạo hàm không chỉ là một công cụ để giải các bài tập toán học mà còn có rất nhiều ứng dụng trong thực tế, như:
Câu 4 trang 223 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài tập này và tự tin hơn trong quá trình học tập.