Chào mừng bạn đến với bài tập trắc nghiệm Hình học 11 Nâng cao, tập trung vào các câu hỏi từ 1 đến 12 trên trang 35 và 36 của sách giáo khoa. Bài tập này được thiết kế để giúp bạn củng cố kiến thức về các khái niệm và định lý quan trọng trong chương trình học.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, kèm đáp án chi tiết và lời giải thích rõ ràng, giúp bạn hiểu sâu sắc hơn về từng dạng bài.
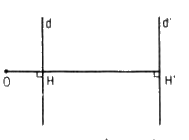
Cho hai đường thẳng song song d và d’.
Cho hai đường thẳng song song d và d’. Có bao nhiêu phép tịnh tiến biến d thành d’
A. Không có phép tịnh tiến nào
B. Có duy nhất một phép tịnh tiến
C. Chỉ có hai phép tịnh tiến
D. Có vô số phép tịnh tiến
Lời giải chi tiết:
Lấy A ∈ d, A’ ∈ d’ thì phép tịnh tiến vecto \(\overrightarrow {AA'} \) biến d thành d’
Chọn D
Cho bốn đường thẳng a, b , a’, b’ trong đó a // a’, b // b’, a cắt b. Có bao nhiêu phép tịnh tiến biến a và b thành a’ và b’ ?

A. Không có phép tịnh tiến nào
B. Có duy nhất một phép tịnh tiến
C. Chỉ có hai phép tịnh tiến
D. Có rất nhiều phép tịnh tiến
Lời giải chi tiết:
Gọi I là giao điểm của a và b
I’ là giao điểm của a’ và b’
Khi đó phép tịnh tiến vecto \(\overrightarrow {II'} \) biến a, b lần lượt thành a’, b’
Chọn B
Cho hai đường thẳng cắt nhau d và d’. Có bao nhiêu phép đối xứng trục biến d thành d’ ?

A. Không có phép đối xứng trục nào
B. Có duy nhất một phép đối xứng trục
C. Chỉ có hai phép đối xứng trục
D. Có rất nhiều phép đối xứng trục
Lời giải chi tiết:
Hai đường phân giác của góc tạo bởi hai đường thẳng d và d’ là các trục đối xứng trục biến đường thẳng d thành đường thẳng d’
Chọn C
Trong các hình dưới đây, hình nào có bốn trục đối xứng ?

A. Hình bình hành
B. Hình bình hành
C. Hình thoi
D. Hình vuông
Lời giải chi tiết:
Hình vuông có 4 trục đối xứng
Chọn D
Trong các mệnh đề sau, mệnh đề nào sai ?
A. Hình gồm hai đường tròn không bằng nhau có trục đối xứng
B. Hình gồm một đường tròn và một đoạn thẳng tùy ý có trục đối xứng
C. Hình gồm một đường tròn và một đường thẳng tùy ý có trục đối xứng
D. Hình gồm một tam cân và đường tròn ngoại tiếp tam giác đó có trục đối xứng
Lời giải chi tiết:

Chọn B
Trong các hình sau đây, hình nào không có tâm đối xứng ?
A. Hình gồm một đường tròn và một hình chữ nhật nội tiếp
B. Hình gồm một đường tròn và một tam giác đều nội tiếp
C. Hình lục giác đều
D. Hình gồm một hình vuông và đường tròn nội tiếp
Lời giải chi tiết:
Tâm O của đường tròn không là tâm đối xứng của tam giác đều ABC

Chọn B
Cho hình vuông ABCD tâm O. Xét phép quay Q có tâm quay O và góc quay φ. Với giá trị nào sau đây của φ, phép quay Q biến hình vuông ABCD thành chính nó ?
A.\(\varphi = {\pi \over 6}\) B.\(\varphi = {\pi \over 4}\)
C.\(\varphi = {\pi \over 3}\) D.\(\varphi = {\pi \over 2}\)
Lời giải chi tiết:
Xét phép quay Q tâm O, góc \({\pi \over 2}\) ta có:

Q: A → B
B → C
C → D
D → A
Suy ra Q: ABCD → ABCD
Chọn D
Cho hai đường thẳng song song d và d’. Có bao nhiêu phép vị tự với tỉ số k = 100 biến d thành d’ ?
A. Không có phép nào
B. Có duy nhất một phép
C. Chỉ có hai phép
D. Có rất nhiều phép

Lời giải chi tiết:
Trên đường thẳng HH’ ⊥ d (H ∈ d, H’ ∈ d’)
Lấy O sao cho \(\overrightarrow {OH'} = 100\,\,\overrightarrow {OH} \)
Phép vị tự tâm O tỉ số k biến d thành d’
Chọn D
Cho đường tròn (O ; R). Tìm mệnh đề sai trong các mệnh đề sau đây:
A. Có phép tịnh tiến biến (O ; R) thành chính nó
B. Có hai phép vị tự biến (O ; R) thành chính nó
C. Có phép đối xứng trục biến (O ; R) thành chính nó
D. Trong ba mệnh đề A, B, C, có ít nhất một mệnh đề sai
Lời giải chi tiết:
A, B, C đều đúng.
Chọn D
Trong các mệnh đề sau đây, mệnh đề nào sai ?
A. Tâm vị tự ngoài của hai đường tròn nằm ngoài hai đường tròn đó
B. Tâm vị tự ngoài của hai đường tròn không nằm giữa hai tâm của hai đường tròn đó
C. Tâm vị tự trong của hai đường tròn luôn thuộc đoạn thẳng nối tâm hai đường tròn đó
D. Tâm vị tự của hai đường tròn có thể là điểm chung của cả hai đường tròn đó
Lời giải chi tiết:
Chọn A
Phép biến hình nào sau đây không có tính chất: “Biến một đường thẳng thành đường thẳng song song hoặc trùng với nó” ?
A. Phép tịnh tiến
B. Phép đối xứng tâm
C. Phép đối xứng trục
D. Phép vị tự
Lời giải chi tiết:
Chọn C
Trong các mệnh đè sau đây, mệnh đề nào sai ?
A. Phép dời hình là một phép đồng dạng
B. Phép vị tự là một phép đồng dạng
C. Phép đồng dạng là một phép dời hình
D. Có phép vị tự không phải là phép dời hình
Lời giải chi tiết:
Chọn C
Chương 1 của SGK Hình học 11 Nâng cao tập trung vào việc xây dựng khái niệm vectơ trong không gian ba chiều, các phép toán vectơ và ứng dụng của vectơ trong việc giải quyết các bài toán hình học. Các câu hỏi từ 1 đến 12 trang 35, 36 chủ yếu xoay quanh các nội dung sau:
Các câu hỏi này thường yêu cầu học sinh xác định các yếu tố của vectơ, thực hiện các phép toán cộng, trừ vectơ, hoặc kiểm tra sự bằng nhau của hai vectơ. Để giải quyết các câu hỏi này, học sinh cần nắm vững định nghĩa và các tính chất cơ bản của vectơ.
Ví dụ: Cho hai vectơ a = (1; 2; 3) và b = (4; 5; 6). Tính a + b.
Giải:a + b = (1 + 4; 2 + 5; 3 + 6) = (5; 7; 9)
Các câu hỏi này tập trung vào việc biểu diễn vectơ bằng tọa độ, tìm tọa độ của điểm, hoặc xác định vị trí tương đối của các điểm trong không gian. Học sinh cần thành thạo các công thức liên quan đến hệ tọa độ và các phép toán vectơ trong hệ tọa độ.
Ví dụ: Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; 3). Tìm tọa độ của điểm B sao cho AB = (2; -1; 0).
Giải: Gọi tọa độ của điểm B là (x; y; z). Ta có AB = (x - 1; y - 2; z - 3). Suy ra x - 1 = 2, y - 2 = -1, z - 3 = 0. Vậy B(3; 1; 3).
Các câu hỏi này yêu cầu học sinh sử dụng kiến thức về vectơ để chứng minh đẳng thức vectơ, tìm tọa độ điểm, hoặc xác định vị trí tương đối của các điểm. Để giải quyết các câu hỏi này, học sinh cần kết hợp kiến thức về vectơ và các định lý hình học.
Ví dụ: Cho tam giác ABC với A(1; 2; 3), B(4; 5; 6), C(7; 8; 9). Chứng minh rằng A, B, C thẳng hàng.
Giải: Ta có AB = (3; 3; 3) và AC = (6; 6; 6). Vì AC = 2AB nên ba điểm A, B, C thẳng hàng.
Việc luyện tập thường xuyên với các bài tập trắc nghiệm là một phương pháp hiệu quả để củng cố kiến thức và nâng cao kỹ năng giải toán. Hy vọng bộ đề trắc nghiệm Câu 1 - 12 trang 35, 36 SGK Hình học 11 Nâng cao trên giaitoan.edu.vn sẽ giúp bạn đạt kết quả tốt trong các kỳ thi sắp tới.