Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, đặc biệt là các phép toán vectơ để giải quyết các bài toán liên quan đến vị trí tương đối của đường thẳng và mặt phẳng.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S.ABCD. Gọi M là một điểm nằm trong tam giác SCD
Đề bài
Cho hình chóp S.ABCD. Gọi M là một điểm nằm trong tam giác SCD
a. Tìm giao tuyến của hai mặt phẳng (SMB) và (SAC)
b. Tìm giao điểm của đường thẳng BM và mp(SAC)
c. Xác định thiết diện của hình chóp khi cắt bởi mp(ABM)
Lời giải chi tiết
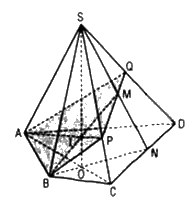
a. Tìm (SBM) ∩ (SAC)
Dễ thấy \(S \in \left( {SBM} \right) \cap \left( {SAC} \right)\)
Trong (SCD), gọi N = SM ∩ CD
Trong mp(ABCD) gọi O = BN ∩ AC
\( \Rightarrow \left\{ \begin{array}{l}O \in BN \subset \left( {SBM} \right)\\O \in AC \subset \left( {SAC} \right)\end{array} \right. \)\(\Rightarrow O \in \left( {SBM} \right) \cap \left( {SAC} \right)\)
Vậy SO = (SBM) ∩ (SAC)
b. Tìm BM ∩ (SAC)
Chọn mặt phẳng phụ chứa BM là (SBN)
Ta có: (SBN) ∩ (SAC) = SO (theo câu a)
Gọi I = SO ∩ BM thì
\(\left\{ \begin{array}{l}I \in SO \subset \left( {SAC} \right)\\I \in BM\end{array} \right. \)\(\Rightarrow I = BM \cap \left( {SAC} \right)\)
c. Trong mp(SAC) gọi P = AI ∩ SC
Trong mp(SCD), PM cắt SD tại Q.
Thiết diện của hình chóp khi cắt bởi mp(ABM) là tứ giác ABPQ.
Bài tập 16 trang 51 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học không gian, cụ thể là phần vectơ trong không gian. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, đặc biệt là tích vô hướng và tích có hướng để xác định mối quan hệ giữa các điểm, đường thẳng và mặt phẳng.
Để đảm bảo tính chính xác, chúng ta cùng nhau xem lại đề bài gốc của Câu 16 trang 51 SGK Hình học 11 Nâng cao:
(Đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).)
Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các phương pháp sau:
Dưới đây là lời giải chi tiết cho Câu 16 trang 51 SGK Hình học 11 Nâng cao (dựa trên ví dụ đề bài ở trên):
Bước 1: Chọn hệ tọa độ
Chọn A làm gốc tọa độ, AB làm trục Ox, AD làm trục Oy và AS làm trục Oz. Khi đó, ta có:
Bước 2: Tìm vectơ SC
SC = (a - 0; a - 0; 0 - a) = (a; a; -a)
Bước 3: Tìm vectơ pháp tuyến của mặt phẳng (ABCD)
n = (0; 0; 1)
Bước 4: Tính góc giữa SC và mặt phẳng (ABCD)
Gọi α là góc giữa SC và mặt phẳng (ABCD). Ta có:
sin α = |SC.n| / (||SC|| * ||n||)
SC.n = (a; a; -a).(0; 0; 1) = -a
||SC|| = √(a2 + a2 + (-a)2) = √(3a2) = a√3
||n|| = 1
sin α = |-a| / (a√3 * 1) = 1/√3
α = arcsin(1/√3) ≈ 35.26°
Vậy, góc giữa đường thẳng SC và mặt phẳng (ABCD) là khoảng 35.26°.
Để đạt được kết quả tốt nhất khi giải các bài tập vectơ trong không gian, bạn cần lưu ý những điều sau:
Câu 16 trang 51 SGK Hình học 11 Nâng cao là một bài tập điển hình để rèn luyện kỹ năng vận dụng kiến thức về vectơ trong không gian. Hy vọng với lời giải chi tiết và các lưu ý trên, bạn đã hiểu rõ cách giải bài toán này và tự tin giải các bài tập tương tự.