Bài toán này thường yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm, hoặc các khái niệm khác đã học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trên tia Ox
Đề bài
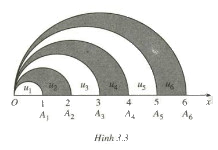
Trên tia Ox lấy các điểm A1, A2, …, An, … sao cho với mỗi số nguyên dương n, OAn = n. Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính OAn, n = 1, 2, … . Kí hiệu u1 là diện tích của nửa hình tròn đường kính OA1 và với mỗi n ≥ 2, kí hiệu un là diện tích của hình giới hạn bởi nửa đường tròn đường kính OAn – 1 , nửa đường tròn đường kính OAn và tia Ox (h 3.3). Chứng minh rằng dãy số (un) là một cấp số cộng. Hãy xác định công sai của cấp số cộng đó.
Lời giải chi tiết
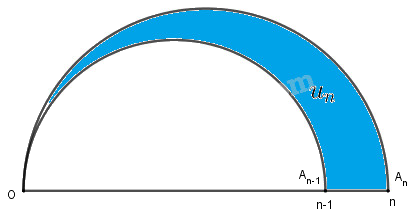
Với \(n ≥ 2\) ta có :
Diện tích nửa đường tròn đường kính \(OA_n\) là: \({S_n} = \frac{1}{2}\pi .{\left( {\frac{{O{A_n}}}{2}} \right)^2} = \frac{1}{8}\pi {n^2}\)
Diện tích nửa đường tròn đường kính \(OA_{n-1}\) là: \({S_{n-1}} = \frac{1}{2}\pi .{\left( {\frac{{O{A_{n-1}}}}{2}} \right)^2} = \frac{1}{8}\pi {(n-1)^2}\)
Do đó,
\(\eqalign{& {u_n} ={S_n} - {S_{n-1}}\cr& = \frac{1}{8}\pi {n^2} - \frac{1}{8}\pi {\left( {n - 1} \right)^2} \cr & = {1 \over 8}\pi \left[ {\left( {{n^2} - {{\left( {n - 1} \right)}^2}} \right)} \right] \cr & = \frac{1}{8}\pi \left( {{n^2} - {n^2} + 2n - 1} \right)\cr&= {{\left( {2n - 1} \right)\pi } \over 8}\,\left( {n \ge 2} \right) \cr & \Rightarrow {u_{n + 1}} - {u_n} \cr&= {{2n + 1} \over 8}\pi - {{\left( {2n - 1} \right)} \over 8}\pi \cr&= {\pi \over 4},\forall n \ge 2 \cr} \)
Mặt khác
\({u_2} - {u_1} = {{3\pi } \over 8} - {\pi \over 8} = {\pi \over 4}\)
Vậy \({u_{n + 1}} - {u_n} = {\pi \over 4}\;\forall n \in\mathbb N^*\)
Do đó (un) là cấp số cộng với công sai \(d = {\pi \over 4}.\)
Câu 20 trang 114 SGK Đại số và Giải tích 11 Nâng cao thường thuộc các dạng bài tập về ứng dụng đạo hàm để khảo sát hàm số, tìm cực trị, hoặc giải phương trình, bất phương trình. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, điều kiện cần và đủ để hàm số đạt cực trị, và các phương pháp giải phương trình, bất phương trình thường gặp.
Trước khi bắt đầu giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Xác định hàm số cần khảo sát, các điều kiện ràng buộc, và mục tiêu cần đạt được (ví dụ: tìm cực trị, tìm khoảng đơn điệu, giải phương trình). Việc phân tích đề bài kỹ lưỡng sẽ giúp bạn định hướng giải quyết bài toán một cách chính xác.
Giả sử đề bài yêu cầu khảo sát hàm số y = x3 - 3x2 + 2. Chúng ta sẽ áp dụng các bước giải trên để giải quyết bài toán này.
Bước 1: Tính đạo hàm cấp nhất: y' = 3x2 - 6x
Bước 2: Tìm các điểm cực trị: Giải phương trình 3x2 - 6x = 0, ta được x = 0 và x = 2.
Bước 3: Xác định loại cực trị: y'' = 6x - 6. Tại x = 0, y'' = -6 < 0, nên hàm số đạt cực đại tại x = 0. Tại x = 2, y'' = 6 > 0, nên hàm số đạt cực tiểu tại x = 2.
Bước 4: Tìm các khoảng đơn điệu: Hàm số đồng biến trên các khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2).
Các bài toán về ứng dụng đạo hàm để khảo sát hàm số có nhiều ứng dụng thực tế trong các lĩnh vực như kinh tế, kỹ thuật, và khoa học tự nhiên. Ví dụ, trong kinh tế, đạo hàm có thể được sử dụng để tìm điểm tối ưu hóa lợi nhuận hoặc chi phí. Trong kỹ thuật, đạo hàm có thể được sử dụng để tính tốc độ thay đổi của các đại lượng vật lý.
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong SGK Đại số và Giải tích 11 Nâng cao hoặc các tài liệu tham khảo khác. Hãy chú trọng vào việc phân tích đề bài, áp dụng các bước giải một cách chính xác, và kiểm tra kết quả.
Câu 20 trang 114 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán về ứng dụng đạo hàm. Bằng cách nắm vững các kiến thức cơ bản và áp dụng các bước giải một cách cẩn thận, bạn có thể tự tin giải quyết bài toán này và các bài toán tương tự.