Bài toán này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm, cực trị của hàm số để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tìm đạo hàm của các hàm số sau :
\(y = 5\sin x - 3\cos x\)
Phương pháp giải:
Sử dụng các công thức (sinx)'=cosx và (cosx)'=-sinx.
Lời giải chi tiết:
\(y' = 5\cos x + 3\sin x\)
\(y = \sin \left( {{x^2} - 3x + 2} \right)\)
Phương pháp giải:
Sử dụng công thức (sinu)'=u'cosu
Lời giải chi tiết:
\(y'=\left[ {\sin \left( {{x^2} - 3x + 2} \right)} \right]' \) \(= \left( {{x^2} - 3x + 2} \right)'\cos \left( {{x^2} - 3x + 2} \right)\) \(= \left( {2x - 3} \right)\cos \left( {{x^2} - 3x + 2} \right)\)
\(y = \cos \sqrt {2x + 1} \)
Phương pháp giải:
Sử dụng công thức (cosu)'=-u'sinu
Lời giải chi tiết:
\(y' = - \left( {\sqrt {2x + 1} } \right)'\sin \sqrt {2x + 1}\) \( = - \frac{{\left( {2x + 1} \right)'}}{{2\sqrt {2x + 1} }}\sin \sqrt {2x + 1} \) \(= -{2 \over {2\sqrt {2x + 1} }}\left( { \sin \sqrt {2x + 1} } \right)\) \( = {{ - \sin \sqrt {2x + 1} } \over {\sqrt {2x + 1} }}\)
\(y = 2\sin 3x\cos 5x\)
Phương pháp giải:
Biến đổi tích thành tổng và tính đạo hàm.
Lời giải chi tiết:
\(y = 2.\frac{1}{2}\left[ {\sin \left( {3x + 5x} \right) + \sin \left( {3x - 5x} \right)} \right] \) \(= \sin 8x + \sin \left( { - 2x} \right)\) \(= \sin 8x - \sin 2x \) \(\Rightarrow y' = \left( {8x} \right)'\cos 8x - \left( {2x} \right)'\cos 2x\) \(= 8\cos 8x - 2\cos 2x\)
\(y = {{\sin x + \cos x} \over {\sin x - \cos x}}\)
Phương pháp giải:
Sử dụng công thức đạo hàm của một thương \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\)
Lời giải chi tiết:
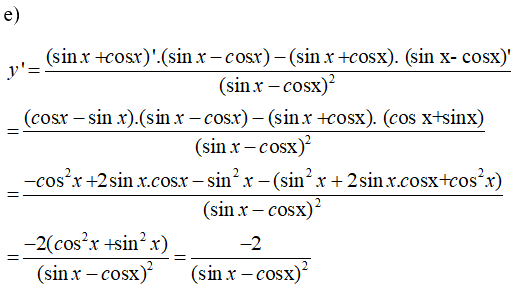
\(y = \sqrt {\cos 2x} \)
Phương pháp giải:
Sử dụng công thức \(\left( {\sqrt u } \right)' = \frac{{u'}}{{2\sqrt u }}\)
Lời giải chi tiết:
\(y' = \frac{{\left( {\cos 2x} \right)'}}{{2\sqrt {\cos 2x} }} = \frac{{\left( {2x} \right)'.\left( { - \sin 2x} \right)}}{{2\sqrt {\cos 2x} }}\) \(= {{ - 2\sin 2x} \over {2\sqrt {\cos 2x} }} = {-{\sin 2x} \over {\sqrt {\cos 2x} }}\)
Câu 29 trang 211 SGK Đại số và Giải tích 11 Nâng cao thường xoay quanh việc tìm cực trị của hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, điều kiện cần và đủ để hàm số đạt cực trị, và các phương pháp xét dấu đạo hàm.
Để giải Câu 29 trang 211, trước hết, cần xác định rõ hàm số cần xét. Thông thường, bài toán sẽ cho một hàm số cụ thể, ví dụ: f(x) = x3 - 3x2 + 2. Sau đó, thực hiện các bước sau:
Giả sử hàm số f(x) = x3 - 3x2 + 2. Ta thực hiện các bước sau:
Các bài toán về cực trị của hàm số có nhiều ứng dụng thực tế, ví dụ như tìm giá trị lớn nhất, giá trị nhỏ nhất của một đại lượng nào đó. Để nâng cao kỹ năng giải toán, bạn có thể luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác.
Việc nắm vững lý thuyết và thực hành giải nhiều bài tập sẽ giúp bạn tự tin hơn trong các kỳ thi và ứng dụng kiến thức vào cuộc sống.
| Điểm | Giá trị |
|---|---|
| Cực đại | (0, 2) |
| Cực tiểu | (2, -2) |