Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và các tính chất hình học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
a. Cho tứ diện ABCD có AB ⊥ CD, AC ⊥ BD. Chứng minh rằng AD ⊥ BC. Vậy, các cạnh đối diện của tứ diện đó vuông góc với nhau. Tứ diện như thế gọi là tứ diện trực tâm.
Đề bài
a. Cho tứ diện ABCD có AB ⊥ CD, AC ⊥ BD. Chứng minh rằng AD ⊥ BC. Vậy, các cạnh đối diện của tứ diện đó vuông góc với nhau. Tứ diện như thế gọi là tứ diện trực tâm.
b. Chứng minh các mệnh đề sau đây là tương đương :
i. ABCD là tứ diện trực tâm.
ii. Chân đường cao của tứ diện hạ từ một đỉnh trùng với trực tâm của mặt đối diện.
iii. \(A{B^2} + C{D^2} = A{C^2} + B{D^2} = A{D^2} + B{C^2}\)
c. Chứng minh rằng bốn đường cao của tứ diện trực tâm đồng quy tại một điểm. Điểm đó gọi là trực tâm của tứ diện nói trên.
Lời giải chi tiết
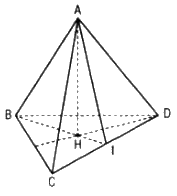
a. Kẻ AH ⊥ (BCD), H ϵ (BCD)
Ta có \(\left\{ {\matrix{ {CD \bot AH} \cr {CD \bot AB} \cr } } \right. \Rightarrow CD \bot \left( {ABH} \right)\)
Mà BH ⊂ (ABH) nên CD ⊥ BH (1)
Tương tự \(\left\{ {\matrix{ {BD \bot AH} \cr {BD \bot AC} \cr } } \right. \Rightarrow BD \bot \left( {ACH} \right) \Rightarrow BD \bot CH\,\left( 2 \right)\)
Từ (1) và (2) suy ra H là trực tâm tam giác BCD.
Ta có: \(\left\{ {\matrix{ {BC \bot AH} \cr {BC \bot DH} \cr } } \right. \Rightarrow BC \bot \left( {ADH} \right) \Rightarrow BC \bot AD.\)
b. Theo chứng minh câu a ta có i ⇔ ii
Mặt khác ta có
\(\eqalign{ & A{B^2} + C{D^2} = A{C^2} + B{D^2} \cr & \Leftrightarrow {\overrightarrow {AB} ^2} + {\overrightarrow {CD} ^2} = {\overrightarrow {AC} ^2} + {\overrightarrow {BD} ^2} \cr & \Leftrightarrow {\overrightarrow {AB} ^2} + {\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right)^2} = {\overrightarrow {AC} ^2} + {\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right)^2} \cr & \Leftrightarrow \overrightarrow {AD} .\overrightarrow {AC} = \overrightarrow {AD} .\overrightarrow {AB} \cr & \Leftrightarrow \overrightarrow {AD} .\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = 0 \cr & \Leftrightarrow \overrightarrow {AD} .\overrightarrow {BC} = 0 \Leftrightarrow AD \bot BC \cr} \)
Tương tự AB ⊥ CD và AC ⊥ BD
Vậy i ⇔ iii
c. Gọi K là trực tâm tam giác ACD thì K nằm trên AI (với BI ⊥ CD). Từ đó suy ra AH và BK cắt nhau do chúng thuộc mp(ABI)
tương tự bốn đường cao của tứ diện trực tâm cắt nhau đôi một và không cùng nằm trên một mặt phẳng nên chúng đồng quy.
Câu 20 trang 103 SGK Hình học 11 Nâng cao thường thuộc vào các dạng bài tập liên quan đến vectơ trong không gian, đặc biệt là các bài toán chứng minh đẳng thức vectơ, tìm mối quan hệ giữa các vectơ, hoặc xác định vị trí tương đối của các điểm trong không gian.
Trước khi bắt đầu giải, điều quan trọng là phải đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Phân tích đề bài giúp ta định hướng phương pháp giải phù hợp.
Để giải quyết Câu 20 trang 103, học sinh cần nắm vững các kiến thức sau:
Có nhiều phương pháp giải khác nhau tùy thuộc vào từng dạng bài tập cụ thể. Một số phương pháp thường được sử dụng:
Giả sử đề bài yêu cầu chứng minh rằng với ba điểm A, B, C bất kỳ, ta có: AB + BC = AC.
Lời giải:
Theo quy tắc cộng vectơ, nếu B là điểm nằm giữa A và C thì AB + BC = AC. Điều này có nghĩa là vectơ AB và vectơ BC cộng lại sẽ cho vectơ AC.
Để củng cố kiến thức và kỹ năng giải toán, bạn nên luyện tập thêm các bài tập tương tự. Dưới đây là một số bài tập gợi ý:
Khi giải các bài toán về vectơ, hãy chú ý đến việc vẽ hình để hình dung rõ hơn về bài toán. Sử dụng các quy tắc và tính chất của vectơ một cách linh hoạt để giải quyết bài toán một cách hiệu quả.
Câu 20 trang 103 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng giải toán về vectơ. Bằng cách nắm vững kiến thức và phương pháp giải, bạn có thể tự tin giải quyết các bài toán tương tự.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Phép cộng vectơ | Quy tắc hình bình hành hoặc quy tắc tam giác. |
| Tích của một số thực với một vectơ | Thay đổi độ dài của vectơ. |