Giải Câu 56 Trang 221 SGK Đại số và Giải tích 11 Nâng cao

Câu 56 trang 221 SGK Đại số và Giải tích 11 Nâng cao

Câu 56 trang 221 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học.

Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết các bài toán thực tế.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.

Cho parabol (P) :

Đề bài

Cho parabol (P) : \(y = {x^2}.\) Gọi M₁ và M₂ là hai điểm thuộc (P), lần lượt có hoành độ là x₁ = -2 và x₂ = 1.

Hãy tìm trên (P) một điểm C sao cho tiếp tuyến tại C song song với cát tuyến M₁M₂. Viết phương trình của tiếp tuyến đó.

Lời giải chi tiết

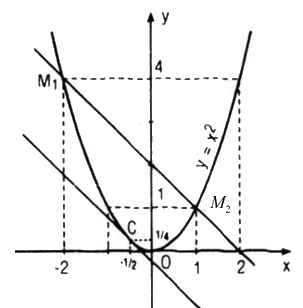
Câu 56 trang 221 SGK Đại số và Giải tích 11 Nâng cao 1

Các điểm M₁ và M₂ có tọa độ là M₁(-2 ; 4); M₂(1 ; 1)

Hệ số góc của cát tuyến M₁M₂ là \(\tan \varphi = {{\Delta y} \over {\Delta x}} = {{4 - 1} \over { - 2 - 1}} = - 1\)

Vì tiếp tuyến tại điểm \(C\left( {{x_0};x_0^2} \right)\) song song với cát tuyến M₁M₂ nên ta có :

\(y'\left( {{x_0}} \right) = - 1 \Leftrightarrow 2{x_0} = - 1 \Leftrightarrow {x_0} = {{ - 1} \over 2},\)

Suy ra tọa độ của điểm C là \(\left( { - {1 \over 2};{1 \over 4}} \right)\)

Vậy phương trình tiếp tuyến phải tìm là :

\(y = \left( { - 1} \right)\left( {x + {1 \over 2}} \right) + {1 \over 4} \Leftrightarrow y = - x - {1 \over 4}\)

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Câu 56 trang 221 SGK Đại số và Giải tích 11 Nâng cao – hành trang không thể thiếu trong chuyên mục toán lớp 11 trên nền tảng toán học. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Câu 56 Trang 221 SGK Đại số và Giải tích 11 Nâng cao: Phân tích Chi Tiết và Lời Giải

Câu 56 trang 221 trong sách giáo khoa Đại số và Giải tích 11 Nâng cao thường xoay quanh các bài toán liên quan đến đạo hàm của hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, bao gồm đạo hàm của hàm số tại một điểm, đạo hàm của các hàm số sơ cấp, và các quy tắc tính đạo hàm (quy tắc cộng, trừ, nhân, chia, hàm hợp).

I. Tóm Tắt Lý Thuyết Liên Quan

Trước khi đi vào giải chi tiết, chúng ta cùng ôn lại một số kiến thức lý thuyết quan trọng:

Đạo hàm của hàm số: Đạo hàm của hàm số f(x) tại điểm x₀, ký hiệu là f'(x₀), là giới hạn của tỷ số \frac{f(x) - f(x_0)}{x - x_0} khi x tiến tới x₀.
Đạo hàm của các hàm số sơ cấp:
- Đạo hàm của hàm số hằng: (c)' = 0
- Đạo hàm của hàm số lũy thừa: (xⁿ)' = nx^n-1
- Đạo hàm của hàm số mũ: (e^x)' = e^x
- Đạo hàm của hàm số logarit: (ln x)' = \frac{1}{x}
Quy tắc tính đạo hàm:
- (u + v)' = u' + v'
- (u - v)' = u' - v'
- (uv)' = u'v + uv'
- (\frac{u}{v})' = \frac{u'v - uv'}{v^2}
- (f(g(x)))' = f'(g(x)) * g'(x)

II. Phân Tích Bài Toán Câu 56 Trang 221

Thông thường, câu 56 trang 221 sẽ yêu cầu học sinh thực hiện một trong các nhiệm vụ sau:

Tính đạo hàm của một hàm số phức tạp.
Tìm điểm cực trị của hàm số.
Khảo sát sự biến thiên của hàm số.
Giải phương trình hoặc bất phương trình chứa đạo hàm.

Để giải quyết bài toán, học sinh cần:

Đọc kỹ đề bài và xác định rõ yêu cầu.
Phân tích hàm số và lựa chọn phương pháp tính đạo hàm phù hợp.
Thực hiện các phép tính đạo hàm một cách chính xác.
Kiểm tra lại kết quả và đảm bảo tính hợp lý.

III. Lời Giải Chi Tiết (Ví dụ Minh Họa)

Giả sử bài toán Câu 56 trang 221 có nội dung như sau:

Cho hàm số y = x³ - 3x² + 2. Hãy tìm các điểm cực trị của hàm số.

Lời giải:

Tính đạo hàm cấp nhất: y' = 3x² - 6x
Tìm điểm dừng: Giải phương trình y' = 0, ta được 3x² - 6x = 0 => x = 0 hoặc x = 2
Tính đạo hàm cấp hai: y'' = 6x - 6
Xác định điểm cực trị:
- Tại x = 0: y'' = -6 < 0 => Hàm số đạt cực đại tại x = 0, y = 2
- Tại x = 2: y'' = 6 > 0 => Hàm số đạt cực tiểu tại x = 2, y = -2

Vậy hàm số đạt cực đại tại điểm (0; 2) và đạt cực tiểu tại điểm (2; -2).