Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và các tính chất hình học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của hai đường thẳng AB’ và A’B. Chứng minh rằng các đường thẳng GI và CG’ song song với nhau.
Đề bài
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của hai đường thẳng AB’ và A’B. Chứng minh rằng các đường thẳng GI và CG’ song song với nhau.
Lời giải chi tiết
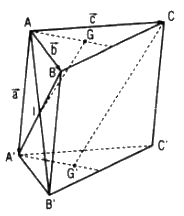
Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \)
Thì \(\overrightarrow {AG} = {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right),\overrightarrow {AI} = {1 \over 2}\left( {\overrightarrow a + \overrightarrow b } \right)\)
Do đó, \(\overrightarrow {GI} = \overrightarrow {AI} - \overrightarrow {AG} = {{3\overrightarrow a + \overrightarrow b - 2\overrightarrow c } \over 6}\)
Mặt khác : \(\overrightarrow {AG'} = {1 \over 3}\left( {\overrightarrow {AA'} + \overrightarrow {AB'} + \overrightarrow {AC'} } \right) = \overrightarrow a + {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right)\)
\( \Rightarrow \overrightarrow {CG'} = \overrightarrow {AG'} - \overrightarrow {AC} = \overrightarrow a + {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right) - \overrightarrow c \)
\(= {{3\overrightarrow a + \overrightarrow b - 2\overrightarrow c } \over 3}\)
Vậy \(\overrightarrow {CG'} = 2\overrightarrow {GI} .\) Ngoài ra, điểm G không thuộc đường thẳng CG’ nên GI và CG’ là hai đường thẳng song song.
Bài toán Câu 3 trang 91 SGK Hình học 11 Nâng cao thường xoay quanh việc áp dụng các kiến thức về vectơ trong không gian, đặc biệt là các phép toán vectơ như cộng, trừ, nhân với một số thực, và tích vô hướng. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững định nghĩa, tính chất của vectơ, cũng như các công thức liên quan đến tích vô hướng.
Trước khi đi vào giải chi tiết, chúng ta cần ôn lại một số kiến thức cơ bản:
Thông thường, bài toán này sẽ cho trước một số vectơ hoặc các điểm trong không gian. Yêu cầu có thể là:
Để giải quyết bài toán, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu cần tìm. Sau đó, vận dụng các kiến thức và công thức đã học để xây dựng lời giải.
Giả sử đề bài yêu cầu:
Cho hình hộp ABCD.A'B'C'D'. Biết AB = a, AD = b, AA' = c. Tính tích vô hướng của các vectơ AB và AD.
Lời giải:
Vì ABCD là hình hộp nên AB vuông góc với AD. Do đó, tích vô hướng của AB và AD bằng 0.
AB.AD = 0
Ngoài bài toán Câu 3 trang 91, còn rất nhiều bài tập tương tự liên quan đến vectơ trong không gian. Một số dạng bài tập thường gặp:
Để giải quyết các bài tập này, học sinh cần:
Kiến thức về vectơ trong không gian có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như vật lý, kỹ thuật, đồ họa máy tính. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán thực tế một cách hiệu quả hơn.
Hy vọng với lời giải chi tiết và các phân tích trên, bạn đã hiểu rõ hơn về cách giải Câu 3 trang 91 SGK Hình học 11 Nâng cao. Hãy luyện tập thêm nhiều bài tập khác để củng cố kiến thức và kỹ năng của mình.