Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đồ thị hàm số và các phép biến đổi đồ thị để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
Xét hàm số a. Chứng minh rằng với mỗi số nguyên k, f(x + k4π) = f(x) với mọi x.
Chứng minh rằng với mỗi số nguyên \(k\), \(f(x + k4π) = f(x)\) với mọi \(x\).
Lời giải chi tiết:
\(f\left( {x + k4\pi } \right) = \cos \frac{{x + k4\pi }}{2}\)
\(= \cos \left( {{x \over 2} + k2\pi } \right) \) \(= \cos {x \over 2} = f\left( x \right)\)
Lập bảng biến thiên của hàm số \(y = \cos {x \over 2}\) trên đoạn \([-2π ; 2π]\).
Lời giải chi tiết:
Bảng biến thiên :
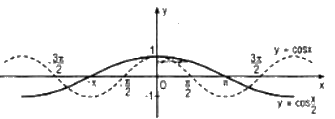
Vẽ đồ thị của các hàm số \(y = \cos x\) và \(y = \cos {x \over 2}\) trong cùng một hệ trục tọa độ vuông góc \(Oxy\).
Lời giải chi tiết:

Trong mặt phẳng tọa độ \(Oxy\), xét phép biến hình \(F\) biến mỗi điểm \((x ; y)\) thành điểm \((x'; y')\) sao cho \(x'= 2x\) và \(y'= y\). Chứng minh rằng F biến đồ thị của hàm số \(y = \cos x\) thành đồ thị của hàm số \(y = \cos {x \over 2}.\)
Lời giải chi tiết:
Ta có:
\(\left\{ \begin{array}{l}x' = 2x\\y' = y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \frac{{x'}}{2}\\y =y'\end{array} \right.\)
Do đó \(y = \cos x\) \( \Leftrightarrow \) \(y' = \cos {{x'} \over 2}\).
Do đó phép biến đổi xác định bởi \((x ; y) ↦ (x' ; y')\) sao cho \(x' = 2x, y'= y\) biến đồ thị hàm số \(y = \cos x\) thành đồ thị hàm số \(y = \cos {x \over 2}.\)

Bài tập 13 trang 17 trong sách giáo khoa Đại số và Giải tích 11 Nâng cao thường xoay quanh việc xét tính đơn điệu của hàm số, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước, hoặc xác định các yếu tố của đồ thị hàm số như điểm cực trị, điểm uốn. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, điều kiện cần và đủ để hàm số đơn điệu, và các phương pháp tìm cực trị.
Trước khi đi vào giải chi tiết bài tập, chúng ta cùng ôn lại một số lý thuyết quan trọng:
Để giải bài tập 13 trang 17, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Sau đó, lập kế hoạch giải cụ thể, bao gồm các bước sau:
Bước 1: Tính đạo hàm cấp nhất
f'(x) = 3x2 - 6x
Bước 2: Tìm các điểm mà f'(x) = 03x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
Bước 3: Lập bảng biến thiên| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Hàm số f(x) đạt cực đại tại x = 0, với giá trị f(0) = 2. Hàm số f(x) đạt cực tiểu tại x = 2, với giá trị f(2) = -2.
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự với các hàm số khác nhau. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững phương pháp giải và tự tin hơn khi làm bài kiểm tra.
Ngoài ra, học sinh có thể tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, chẳng hạn như việc tối ưu hóa lợi nhuận trong kinh doanh, hoặc việc xác định vận tốc và gia tốc trong vật lý.