Bài tập Câu 8 trang 80 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài toán này yêu cầu học sinh vận dụng kiến thức về vectơ, phương trình đường thẳng và các tính chất liên quan để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là tọng tâm tam giác ABC. Cắt tứ diện bởi mp(GCD) thì diện tích của thiết diện là :
Đề bài
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là tọng tâm tam giác ABC. Cắt tứ diện bởi mp(GCD) thì diện tích của thiết diện là :
A. \({{{a^2}\sqrt 3 } \over 2}\)
B. \({{{a^2}\sqrt 2 } \over 4}\)
C. \({{{a^2}\sqrt 2 } \over 6}\)
D. \({{{a^2}\sqrt 3 } \over 4}\)
Lời giải chi tiết
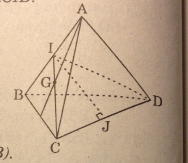
Gọi I là trung điểm của AB. Thiết diện cần tìm là ΔCID
Gọi J là trung điểm CD
ΔCID cân nên IJ ⊥ CD ⇒ \({S_{ICD}} = {1 \over 2}IJ.CD\)
Ta có:
\(\eqalign{ & I{J^2} = C{I^2} - C{J^2} = {\left( {{{a\sqrt 3 } \over 2}} \right)^2} - {{{a^2}} \over 4} = {{{a^2}} \over 2} \cr & \Rightarrow IJ = {{a\sqrt 2 } \over 2} \Rightarrow {S_{ICD}} = {1 \over 2}.{{a\sqrt 2 } \over 2}.a = {{{a^2}\sqrt 2 } \over 4} \cr} \)
Chọn (B)
Câu 8 trang 80 SGK Hình học 11 Nâng cao thường xoay quanh các bài toán liên quan đến việc xác định mối quan hệ giữa các điểm, đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về vectơ, đặc biệt là các phép toán vectơ như cộng, trừ, nhân với một số thực và tích vô hướng.
Để giải Câu 8 trang 80 SGK Hình học 11 Nâng cao, học sinh thường cần thực hiện các bước sau:
Giả sử Câu 8 trang 80 SGK Hình học 11 Nâng cao yêu cầu tìm giao điểm của đường thẳng d và mặt phẳng (P). Để giải bài toán này, ta có thể thực hiện các bước sau:
Ngoài việc tìm giao điểm của đường thẳng và mặt phẳng, Câu 8 trang 80 SGK Hình học 11 Nâng cao còn có thể xuất hiện các dạng bài tập khác như:
Để giải tốt các bài tập về Hình học không gian, học sinh cần:
Học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải bài tập:
Hy vọng với hướng dẫn chi tiết này, học sinh sẽ tự tin giải quyết Câu 8 trang 80 SGK Hình học 11 Nâng cao và các bài tập tương tự một cách hiệu quả.