Chào mừng bạn đến với bài giải chi tiết Câu 15 trang 51 SGK Hình học 11 Nâng cao tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chính xác, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán Hình học 11 Nâng cao.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tự tin đối mặt với mọi bài tập.
Cho hình chóp tứ giác S.ABCD. Ba điểm A’, B’, C’lần lượt nằm trên ba cạnh SA, SB, SC nhưng không trùng với S, A, B, C. Xác định thiết diện của hình chóp khi cắt bởi mp(A’B’C’)
Đề bài
Cho hình chóp tứ giác S.ABCD. Ba điểm A’, B’, C’ lần lượt nằm trên ba cạnh SA, SB, SC nhưng không trùng với S, A, B, C. Xác định thiết diện của hình chóp khi cắt bởi mp(A’B’C’).
Lời giải chi tiết
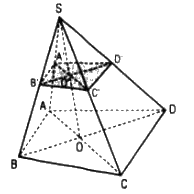
Trong (ABCD), gọi O = AC ∩ BD.
Trong (SAC), gọi O’ = A’C’ ∩ SO.
Trong (SBD), gọi D’ = B’O’ ∩ SD
Nếu D’ thuộc đoạn SD thì thiết diện là tứ giác A’B’C’D’
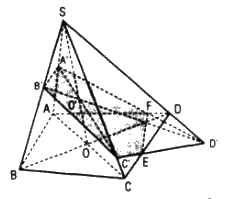
Nếu D’ nằm trên phần kéo dài của cạnh SD, ta gọi E là giao điểm của CD và C'D’, F là giao điểm của AD và A’D’
Do đó thiết diện là ngũ giác A’B’C’EF.
Câu 15 trang 51 SGK Hình học 11 Nâng cao thường xoay quanh các kiến thức về vectơ, đặc biệt là các phép toán vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản như:
Để giải Câu 15 trang 51 SGK Hình học 11 Nâng cao, bạn có thể áp dụng các phương pháp sau:
Giả sử Câu 15 yêu cầu tính góc giữa hai vectơ a = (1; 2; 3) và b = (-2; 1; 0). Ta thực hiện như sau:
Bước 1: Tính tích vô hướng của hai vectơ:
a ⋅ b = (1)(-2) + (2)(1) + (3)(0) = -2 + 2 + 0 = 0
Bước 2: Tính độ dài của mỗi vectơ:
|a| = √(1² + 2² + 3²) = √14
|b| = √((-2)² + 1² + 0²) = √5
Bước 3: Sử dụng công thức tính góc giữa hai vectơ:
cos(θ) = (a ⋅ b) / (|a| |b|) = 0 / (√14 √5) = 0
Suy ra θ = 90°
Vậy góc giữa hai vectơ a và b là 90°.
Câu 15 trang 51 SGK Hình học 11 Nâng cao có thể xuất hiện dưới nhiều dạng khác nhau, bao gồm:
Khi giải các bài tập về vectơ, bạn cần chú ý:
Hy vọng với những phân tích và hướng dẫn chi tiết trên, bạn đã có thể tự tin giải quyết Câu 15 trang 51 SGK Hình học 11 Nâng cao. Hãy luyện tập thường xuyên để nâng cao kiến thức và kỹ năng của mình nhé!