Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và ứng dụng vào hình học không gian.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho tứ diện ABCD. Bốn điểm P, Q, R, S lần lượt nằm trên bốn cạnh AB, BC, CD, DA và không trùng với các đỉnh của tứ diện. Chứng minh rằng
Đề bài
Cho tứ diện ABCD. Bốn điểm P, Q, R, S lần lượt nằm trên bốn cạnh AB, BC, CD, DA và không trùng với các đỉnh của tứ diện. Chứng minh rằng
a. Bốn điểm P, Q, R, S đồng phẳng khi và chỉ khi ba đường thẳng PQ, RS, AC hoặc đôi một song song hoặc đồng quy
b. Bốn điểm P, Q, R, S đồng phẳng khi và chỉ khi ba đường thẳng PS, RQ, BD hoặc đôi một song song hoặc đồng quy
Lời giải chi tiết
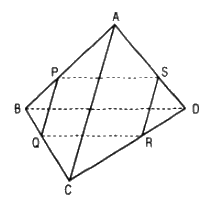
a. Nếu P, Q, R, S đồng phẳng thì chúng cùng thuộc mặt phẳng (PQRS).
Ta có:
(PQRS) ∩ (ABC) = PQ
(PQRS) ∩ (ACD) = RS
(ABC) ∩ (ACD) = AC
Theo định lí về giao tuyến của ba mặt phẳng thì PQ, SR, AC hoặc đôi một song song hoặc đồng quy.
Ngược lại, nếu ba đường thẳng PQ, AC, RS hoặc đôi một song song hoặc đồng quy thì hai đường thẳng PQ và RS cùng thuộc một mặt phẳng, từ đó bốn điểm P, Q, R, S đồng phẳng.
b. Nếu P, Q, R, S đồng phẳng thì chúng cùng thuộc mặt phẳng (PQRS).
Ta có:
(PQRS) ∩ (ABD) = PS
(PQRS) ∩ (BCD) = RQ
(ABD) ∩ (BCD) = BD
Theo định lí về giao tuyến của ba mặt phẳng thì PS, RQ, BD hoặc đôi một song song hoặc đồng quy.
Ngược lại, nếu ba đường thẳng PS, RQ, BD hoặc đôi một song song hoặc đồng quy thì hai đường thẳng PS và RQ cùng thuộc một mặt phẳng, từ đó bốn điểm P, Q, R, S đồng phẳng.
Câu 19 trang 55 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học 11, tập trung vào việc vận dụng kiến thức về vectơ trong không gian để giải quyết các bài toán liên quan đến hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Thông thường, bài toán Câu 19 trang 55 SGK Hình học 11 Nâng cao sẽ yêu cầu học sinh:
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, giải thích rõ ràng và sử dụng hình vẽ minh họa nếu cần thiết. Ví dụ, nếu bài toán yêu cầu chứng minh ba điểm thẳng hàng, lời giải sẽ trình bày các bước sử dụng vectơ để chứng minh điều đó.)
Giả sử bài toán yêu cầu chứng minh rằng ba điểm A, B, C thẳng hàng. Ta có thể sử dụng vectơ để chứng minh điều này bằng cách:
Ngoài việc giải Câu 19 trang 55 SGK Hình học 11 Nâng cao, học sinh nên luyện tập thêm các bài toán tương tự để củng cố kiến thức và kỹ năng. Một số bài tập mở rộng có thể bao gồm:
Khi giải các bài tập về vectơ, học sinh cần lưu ý:
Câu 19 trang 55 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về vectơ vào giải quyết các bài toán hình học không gian. Bằng cách nắm vững các khái niệm cơ bản, phân tích bài toán một cách cẩn thận và thực hành thường xuyên, học sinh có thể tự tin giải quyết các bài toán tương tự.
Hy vọng với lời giải chi tiết và những kiến thức bổ ích trên, các bạn học sinh có thể hiểu rõ hơn về Câu 19 trang 55 SGK Hình học 11 Nâng cao và đạt kết quả tốt trong môn học Hình học.