Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác các bài tập trong sách giáo khoa Hình học 11 Nâng cao.
Trong bài viết này, chúng tôi sẽ cùng nhau giải quyết Câu 8 trang 78 SGK Hình học 11 Nâng cao, giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Hãy cùng bắt đầu với việc phân tích đề bài và tìm ra hướng giải quyết tối ưu nhất.
Cho hai tia Ax và By nằm trên hai đường thẳng chéo nhau. Một điểm M chạy trên Ax và một điểm N chạy trên By sao cho AM = kBN (k > 0 cho trước)
Chứng minh rằng MN song song với một mặt phẳng cố định
Giải chi tiết:
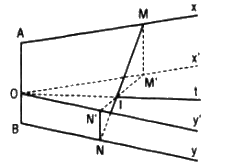
Dựng tia Bz song song và cùng hướng với tia Ax. Trên các tia Ax, By và Bz lần lượt lấy các điểm cố định M0, N0 và M’0 sao cho \({{A{M_0}} \over {B{N_0}}} = k\) và \(BM{'_0} = A{M_0}\)
Khi đó ta có : \({M_0}M{'_0}//AB\) và \({{BM{'_0}} \over {BN_0}} = k\,\,\left( 1 \right)\)
Lấy điểm M’ thuộc tia Bz sao cho BM’ = AM.
Từ (1) và (2) ta có : MM’ // M0M’0 (3)
Và \({{BM'} \over {BN}} = {{B{M'_0}} \over {B{N_0}}}\,\,\left( 4 \right)\)
Từ (4) suy ra NM’ // N0M’0 (5)
Từ (3) và (5) suy ra mp(MNM’) // mp(M0N0M’0).
Vậy MN luôn song song với mặt phẳng cố định (M0N0M’0)
Tìm tập hợp các điểm I thuộc đoạn MN sao cho IM = kIN
Giải chi tiết:

Thuận. Gọi O là một điểm thuộc đoạn thẳng AB sao cho OA : OB = k. Từ O ta vẽ hai tia Ox’ và Oy’ sao cho Ox’ // Ax, Oy’ // By. Xét phép chiếu song song theo phương AB lên mp(Ox’, Oy’). Gọi M’, N’ lần lượt là hình chiếu của M và N theo phép chiếu này. Khi đó, giao điểm của MN và M’N’ chính là điểm I vì rõ ràng ta có :
\({{IM} \over {IN}} = {{M'M} \over {N'N}} = {{OA} \over {OB}} = k\)
Trong tam giác M’ON’, ta có : \({{IM'} \over {IN'}} = k,{{OM'} \over {ON'}} = {{AM} \over {BN}} = k\)
Vậy \({{IM'} \over {IN'}} = {{OM'} \over {ON'}} = k.\) Từ đó suy ra I phải nằm trên tia phân giác Ot của góc x’Oy’.
Đảo. Giả sử I là một điểm bất kì thuộc tia phân giác Ot của góc x’Oy’.
Gọi M’, N’ là những điểm lần lượt thuộc tia Ox’, tia Oy’ sao cho M’, I, N’ thẳng hàng và \({{IM'} \over {IN'}} = k\) (có thể tìm M’, N’ bằng cách dùng phép vị tự tâm I tỉ số -k trên mp(Ox’y’)). Gọi M, N lần lượt là những điểm thuộc các tia Ax, By sao cho AM = OM’, BN = ON’. Dễ thấy I, M, N thẳng hàng và IM : IN = k
Kết luận : Tập hợp các điểm I thỏa mãn điều kiện bài toán là tia phân giác Ot của góc x’Oy’.
Câu 8 trang 78 SGK Hình học 11 Nâng cao thường liên quan đến các kiến thức về vectơ, các phép toán vectơ, và ứng dụng của vectơ trong hình học phẳng. Để giải quyết bài toán này, chúng ta cần nắm vững các định nghĩa, tính chất và công thức liên quan.
Trước khi bắt đầu giải, hãy đọc kỹ đề bài và xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Điều này giúp chúng ta xây dựng một kế hoạch giải quyết bài toán hiệu quả.
(Giả sử đề bài cụ thể là: Cho tam giác ABC có A(1;2), B(3;4), C(-1;0). Tìm tọa độ điểm D sao cho ABCD là hình bình hành.)
Để ABCD là hình bình hành, ta cần có AB = DC và AD = BC. Điều này có nghĩa là vectơ AB = vectơ DC và vectơ AD = vectơ BC.
Ta thấy có sự mâu thuẫn. Điều này có nghĩa là ta cần xét trường hợp ABCD là hình bình hành theo thứ tự khác. Ví dụ, ABDC là hình bình hành.
Lại có sự mâu thuẫn. Vậy ta xét trường hợp ADBC là hình bình hành.
Vậy D(5; 6).
Với đề bài cho, tọa độ điểm D là (5; 6) để ABCD là hình bình hành.
Khi giải các bài toán về vectơ, cần chú ý đến việc xác định đúng hướng của các vectơ và áp dụng đúng các công thức. Việc vẽ hình minh họa cũng rất quan trọng để hình dung rõ bài toán và tìm ra hướng giải quyết.
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong sách giáo khoa hoặc các tài liệu tham khảo khác.