Chào mừng bạn đến với bài giải chi tiết Câu 1 trang 120 SGK Hình học 11 Nâng cao trên giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải đầy đủ, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán Hình học 11.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, hỗ trợ bạn trong quá trình chinh phục môn Toán.
Tứ diện OABC có OA = OB = OC = a và
Đề bài
Tứ diện OABC có OA = OB = OC = a và \(\widehat {AOB} = \widehat {AOC} = 60^\circ ,\widehat {BOC} = 90^\circ \)
a. Chứng tỏ rằng ABC là tam giác vuông và OA ⊥ BC
b. Tìm đường vuông góc chung IJ của OA và BC ; tính khoảng cách giữa hai đường thẳng OA và BC.
c. Chứng minh rằng hai mặt phẳng (ABC) và (OBC) vuông góc với nhau.
Lời giải chi tiết
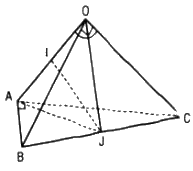
a. Vì \(\widehat {AOB} = \widehat {AOC} = 60^\circ \)
OA = OB = OC = a
Nên AB = AC = a
Suy ra ΔABC = ΔOBC
Vậy tam giác ABC vuông cân tại A
Gọi J là trung điểm của BC thì OJ ⊥ BC, AJ ⊥ BC nên OA ⊥ BC.
Cách khác:

b. Gọi I là trung điểm của OA, do OJ = AJ nên JI ⊥ OA, mà JI ⊥ BC, vậy IJ là đường vuông góc chung của OA và BC.
\(I{J^2} = O{J^2} - O{I^2} = {\left( {{{a\sqrt 2 } \over 2}} \right)^2} - {\left( {{a \over 2}} \right)^2} = {{{a^2}} \over 4}.\)
Suy ra : d(OA ; BC) = \({a \over 2}\)
c. Từ các kết quả trên ta có : OJ ⊥ BC, AJ ⊥ BC, IJ = \({1 \over 2}OA\)
Vậy góc giữa mp(OBC) và mp(ABC) bằng góc \(\widehat {OJA}\) và \(\widehat {OJA} = 90^\circ ,\) do đó mp(OBC) ⊥ mp(ABC).
Câu 1 trang 120 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về vectơ, các phép toán vectơ và ứng dụng của chúng trong hình học không gian. Bài toán này thường kiểm tra khả năng phân tích, tổng hợp và vận dụng kiến thức vào giải quyết vấn đề thực tế.
(Nội dung đề bài sẽ được chèn vào đây. Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).)
Để giải quyết bài toán này, chúng ta cần thực hiện các bước sau:
(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước tính toán cụ thể, giải thích rõ ràng và kết luận chính xác. Ví dụ:)
Gọi A(0;0;0), B(a;0;0), C(a;a;0), D(0;a;0) và S(0;0;a). Khi đó:
Góc giữa đường thẳng SC và mặt phẳng (ABCD) là góc giữa vectơ SC và vectơ pháp tuyến n của mặt phẳng (ABCD). Ta có:
cos(θ) = |SC.n| / (||SC|| * ||n||) = |(a; a; -a).(0; 0; 1)| / (√(a2 + a2 + a2) * √1) = | -a | / (a√3 * 1) = 1/√3
Vậy θ = arccos(1/√3) ≈ 54.74°
Khi giải các bài toán về hình học không gian, cần chú ý:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Hy vọng bài giải chi tiết Câu 1 trang 120 SGK Hình học 11 Nâng cao trên giaitoan.edu.vn đã giúp bạn hiểu rõ hơn về phương pháp giải và nắm vững kiến thức liên quan. Chúc bạn học tập tốt!
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.