Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng để giải quyết các vấn đề thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD và DA. Kẻ MM’, NN’, PP’, QQ’ lần lượt vuông góc với CD, DA, AB, BC.
Đề bài
Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD và DA. Kẻ MM’, NN’, PP’, QQ’ lần lượt vuông góc với CD, DA, AB, BC.
a. Gọi I là giao điểm của MP và NQ. Phép đối xứng tâm ĐI biến các đường thẳng MM’, NN’, PP’, QQ’ thành những đường thẳng nào ?
b. Chứng tỏ rằng bốn đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại một điểm. Nhận xét gì về vị trí điểm đồng quy và hai điểm I, O?
Lời giải chi tiết
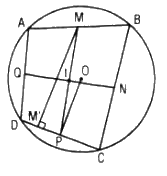
a. MNPQ là hình bình hành nên I là trung điểm
của MP và NQ.
Phép đối xứng tâm ĐI biến điểm M thành điểm P, biến đường thẳng MM’ thành đường thẳng đi qua P và song song với MM’, tức là vuông góc với DC.
Vậy đường thẳng MM’ được biến thành đường thẳng PO. Hoàn toàn tương tự : đường thẳng NN’ biến thành đường QO, đường thẳng PP’ biến thành đường MO, đường thẳng QQ’ biến thành đường NO.
b. Vì bốn đường thẳng MO, NO, PO, QO đồng quy tại điểm O nên bốn đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại O’ đối xứng với O qua điểm I.
Câu 2 trang 124 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học không gian, cụ thể là phần kiến thức về vectơ trong không gian và ứng dụng vào việc xác định mối quan hệ giữa các điểm, đường thẳng và mặt phẳng. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Dưới đây là phân tích chi tiết và lời giải của Câu 2 trang 124 SGK Hình học 11 Nâng cao:
Trước khi bắt đầu giải, hãy đọc kỹ đề bài và xác định rõ các yếu tố quan trọng. Thông thường, đề bài sẽ cung cấp thông tin về các điểm, vectơ hoặc các yếu tố hình học khác. Nhiệm vụ của học sinh là sử dụng các kiến thức đã học để tìm ra mối quan hệ giữa chúng và đưa ra kết quả chính xác.
(Nội dung lời giải chi tiết của Câu 2 trang 124 SGK Hình học 11 Nâng cao sẽ được trình bày tại đây. Lời giải cần bao gồm các bước giải rõ ràng, sử dụng các công thức và định lý phù hợp, và giải thích chi tiết từng bước để học sinh dễ dàng theo dõi và hiểu được.)
Để giúp học sinh hiểu rõ hơn về cách giải bài toán này, chúng ta sẽ xem xét một ví dụ minh họa:
(Ví dụ minh họa sẽ được trình bày tại đây, bao gồm đề bài, lời giải và giải thích chi tiết.)
Ngoài Câu 2 trang 124 SGK Hình học 11 Nâng cao, còn rất nhiều bài tập tương tự khác trong chương trình Hình học không gian. Dưới đây là một số dạng bài tập thường gặp:
Để giải các bài tập về Hình học không gian một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn có thể làm thêm một số bài tập sau:
Câu 2 trang 124 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ trong không gian và ứng dụng vào việc giải quyết các vấn đề thực tế. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn khi đối mặt với các bài toán tương tự.
| Khái niệm | Định nghĩa |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Tích vô hướng | Một phép toán giữa hai vectơ cho ra một số thực. |
| Tích có hướng | Một phép toán giữa hai vectơ cho ra một vectơ vuông góc với cả hai vectơ ban đầu. |
| Bảng tóm tắt các khái niệm quan trọng. | |