Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tứ diện đều ABCD có cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó, diện tích thiết diện của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp(ACD) là:
Đề bài
Cho tứ diện đều ABCD có cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó, diện tích thiết diện của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp(ACD) là:
A. \({{{m^2}\sqrt 3 } \over 4}\)
B. \({{{{\left( {a - m} \right)}^2}\sqrt 2 } \over 2}\)
C. \({{{{\left( {a + m} \right)}^2}} \over 4}\)
D. \({{{{\left( {a - m} \right)}^2}\sqrt 3 } \over 4}\)
Lời giải chi tiết
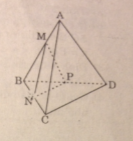
Vẽ MN // AC (N ϵ BC)
MP // AD (P ϵ BD)
Thiết diện cần tìm là ΔMNP
Ta có: \(\Delta MNP\backsim \Delta ACD\) tỉ số \({{MP} \over {AD}} = {{BM} \over {AB}} = {{a - m} \over a}\)
\( \Rightarrow \frac{{{S_{MNP}}}}{{{S_{ACD}}}} = {\left( {\frac{{MP}}{{AD}}} \right)^2} = {\left( {\frac{{a - m}}{a}} \right)^2}\)
\( \Rightarrow {S_{MNP}} = {\left( {{{a - m} \over a}} \right)^2}.{S_{ABC}} \)
\(= {\left( {{{a - m} \over a}} \right)^2}.{{{a^2}\sqrt 3 } \over 4} = {\left( {a - m} \right)^2}{{\sqrt 3 } \over 4}\)
Chọn (D)
Bài tập 11 trang 80 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học 11, tập trung vào việc củng cố kiến thức về vectơ và ứng dụng của chúng trong giải quyết các bài toán hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và đặc biệt là các tính chất của vectơ trong các hình bình hành, tam giác.
Thông thường, bài tập 11 trang 80 SGK Hình học 11 Nâng cao sẽ yêu cầu học sinh chứng minh một đẳng thức vectơ, xác định vị trí tương đối của các điểm, hoặc tính độ dài của một đoạn thẳng dựa trên các vectơ đã cho. Bài toán có thể liên quan đến các hình hình học cơ bản như tam giác, hình bình hành, hình chữ nhật, hoặc các hình phức tạp hơn.
Để giải quyết bài toán này, học sinh có thể áp dụng các phương pháp sau:
Giả sử bài toán yêu cầu chứng minh rằng với tam giác ABC, nếu G là trọng tâm thì GA + GB + GC = 0. Lời giải sẽ như sau:
Vì G là trọng tâm của tam giác ABC, ta có:
Ta biết rằng AD = (AB + AC) / 2, BE = (BA + BC) / 2, và CF = (CA + CB) / 2. Thay các biểu thức này vào các đẳng thức trên, ta có:
GA + GB + GC = 2/3 * (AB + AC) / 2 + 2/3 * (BA + BC) / 2 + 2/3 * (CA + CB) / 2
Rút gọn biểu thức, ta được:
GA + GB + GC = 1/3 * (AB + AC + BA + BC + CA + CB) = 1/3 * (AB + BA + AC + CA + BC + CB) = 1/3 * (0 + 0 + 0) = 0
Vậy, GA + GB + GC = 0.
Xét tam giác ABC với A(0;0), B(2;0), C(0;2). Tìm tọa độ của trọng tâm G và chứng minh GA + GB + GC = 0.
Tọa độ của trọng tâm G là: G = ((0+2+0)/3, (0+0+2)/3) = (2/3, 2/3)
Ta có:
GA + GB + GC = (2/3 - 4/3 + 2/3, 2/3 + 2/3 - 4/3) = (0, 0)
Vậy, GA + GB + GC = 0.
Vectơ là một công cụ mạnh mẽ trong việc giải quyết các bài toán hình học. Chúng được sử dụng để:
Hy vọng với lời giải chi tiết và các phương pháp giải trên, bạn sẽ tự tin hơn khi giải quyết bài tập 11 trang 80 SGK Hình học 11 Nâng cao và các bài tập tương tự khác.