Giải Câu 11 Trang 17 SGK Đại số và Giải tích 11 Nâng cao

Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao

Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học.

Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đồ thị hàm số và các phép biến đổi đồ thị để giải quyết.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Từ đồ thị của hàm số y = sinx, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó :

LG a

\(y = -\sin x\)

Lời giải chi tiết:

Đồ thị của hàm số \(y = -\sin x\) là hình đối xứng qua trục hoành của đồ thị hàm số \(y = \sin x\)

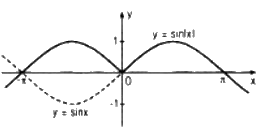
Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao 1

LG b

\(y = \left| {\sin x} \right|\)

Lời giải chi tiết:

Ta có: \(\left| {\sin x} \right| = \left\{ {\matrix{{\sin x\,\text{ nếu }\,\sin x \ge 0} \cr { - \sin x\,\text{ nếu }\,\sin x < 0} \cr} } \right.\)

Do đó đồ thị của hàm số \(y = |\sin x|\) có được từ đồ thị \((C)\) của hàm số \(y = \sin x\) bằng cách:

- Giữ nguyên phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(y ≥ 0\) (tức nửa mặt phẳng bên trên trục hoành kể cả bờ \(Ox\)).

- Lấy hình đối xứng qua trục hoành của phần đồ thị \((C)\) nằm trong nửa mặt phẳng \(y < 0\) (tức là nửa mặt phẳng bên dưới trục hoành không kể bờ \(Ox\));

- Xóa phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(y < 0\).

- Đồ thị \(y = |\sin x|\) là đường liền nét trong hình dưới đây :

Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao 1

LG c

\(y = \sin|x|\)

Lời giải chi tiết:

Ta có: \(\sin \left| x \right| = \left\{ {\matrix{{\sin x\,\text{ nếu }\,x \ge 0} \cr { - \sin x\,\text{ nếu }\,x < 0} \cr} } \right.\)

Do đó đồ thị của hàm số \(y = \sin|x|\) có được từ đồ thị \((C)\) của hàm số \(y = \sin x\) bằng cách :

- Giữ nguyên phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(x ≥ 0\) (tức nửa mặt phẳng bên phải trục tung kể cả bờ \(Oy\)).

- Xóa phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(x < 0\) (tức nửa mặt phẳng bên trái trục tung không kể bờ \(Oy\)).

- Lấy hình đối xứng qua trục tung của phần đồ thị \((C)\) nằm trong nửa mặt phẳng \(x > 0\)

- Đồ thị \(y = \sin|x|\) là đường nét liền trong hình dưới đây :

Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao 1

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao – hành trang không thể thiếu trong chuyên mục toán lớp 11 trên nền tảng soạn toán. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải Chi Tiết Câu 11 Trang 17 SGK Đại số và Giải tích 11 Nâng cao

Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học kỳ I, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định các yếu tố của hàm số, vẽ đồ thị và tìm các điểm đặc biệt trên đồ thị.

Nội Dung Bài Tập

Thông thường, câu 11 trang 17 sẽ đưa ra một hàm số bậc hai có dạng y = ax² + bx + c và yêu cầu:

Xác định hệ số a, b, c.
Tìm tọa độ đỉnh của parabol.
Tìm trục đối xứng của parabol.
Xác định khoảng đồng biến, nghịch biến của hàm số.
Vẽ đồ thị hàm số.
Tìm các điểm mà đồ thị hàm số cắt trục hoành, trục tung.

Phương Pháp Giải

Để giải quyết bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức sau:

Công thức tính tọa độ đỉnh: x_đỉnh = -b/2a, y_đỉnh = -Δ/4a (với Δ = b² - 4ac).
Phương trình trục đối xứng: x = -b/2a.
Khoảng đồng biến, nghịch biến:
- Nếu a > 0: Hàm số nghịch biến trên (-∞; -b/2a) và đồng biến trên (-b/2a; +∞).
- Nếu a < 0: Hàm số đồng biến trên (-∞; -b/2a) và nghịch biến trên (-b/2a; +∞).
Giao điểm với trục tung: Thay x = 0 vào phương trình hàm số để tìm y.
Giao điểm với trục hoành: Giải phương trình ax² + bx + c = 0 để tìm x.

Ví Dụ Minh Họa

Bài tập: Xét hàm số y = 2x² - 8x + 6.

Giải:

Hệ số: a = 2, b = -8, c = 6.
Tọa độ đỉnh: x_đỉnh = -(-8)/(2*2) = 2, y_đỉnh = -((-8)² - 4*2*6)/(4*2) = -1.
Trục đối xứng: x = 2.
Khoảng đồng biến, nghịch biến: Hàm số nghịch biến trên (-∞; 2) và đồng biến trên (2; +∞).
Giao điểm với trục tung: Thay x = 0, ta được y = 6. Vậy giao điểm là (0; 6).
Giao điểm với trục hoành: Giải phương trình 2x² - 8x + 6 = 0, ta được x = 1 và x = 3. Vậy giao điểm là (1; 0) và (3; 0).

Lưu Ý Quan Trọng

Khi vẽ đồ thị hàm số, bạn cần xác định chính xác các yếu tố như tọa độ đỉnh, trục đối xứng, giao điểm với các trục tọa độ. Điều này giúp bạn vẽ được đồ thị chính xác và dễ dàng hơn.

Ngoài ra, bạn cũng cần chú ý đến dấu của hệ số a để xác định chiều mở của parabol (lên trên nếu a > 0, xuống dưới nếu a < 0).

Bài Tập Tương Tự

Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Hãy luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải bài tập về hàm số bậc hai.

Kết Luận

Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp bạn hiểu sâu hơn về hàm số bậc hai và các ứng dụng của nó. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, bạn sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.