Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và các tính chất hình học để giải quyết.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là trọng tâm tam giác ABC.
Đề bài
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là trọng tâm tam giác ABC.
a. Chứng minh rằng SG ⊥ (ABC). Tính SG.
b. Xét mặt phẳng (P) đi qua A và vuông góc với đường thẳng SC. Tìm hệ thức liên hệ giữa a và b để (P) cắt SC tại điểm C1 nằm giữa S và C. Khi đó hãy tính diện tích thiết diện của hình chóp S.ABC khi cắt bởi mp(P).
Lời giải chi tiết
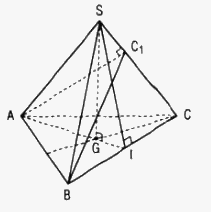
a. Gọi I là trung điểm của BC.
Tam giác ABC đều, AI là đường trung tuyến nên đồng thời là đường cao: BC ⊥ AI.
Tam giác SBC có SB = SC, SI là đường trung tuyến nên đồng thời là đường cao: BC ⊥ SI.
\(\begin{array}{l} \Rightarrow BC \bot (SAI) \supset SG\\ \Rightarrow BC \bot SG.\,\,\, (1)\end{array}\)
Chứng minh tương tự ta có: \(AB \bot SG\,\,\, (1)\)
Từ (1;2) suy ra \(SG \bot (ABC)\)
\(\begin{array}{l}+) \, SI^2 ={S{C^2} - I{C^2}} ={{b^2} - \frac{{{a^2}}}{4}} \\+) \, GI = \frac{1}{3}AI;\, AI ^2 = {A{B^2} - B{I^2}} =a.\frac{{3 }}{4} \Rightarrow GI= \frac{{a\sqrt 3 }}{6}.\end{array}\)
\(\Rightarrow SG = \sqrt {S{I^2} - G{I^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{4} - {{{a^2}} \over {12}}} \) \( = \sqrt {{{12{b^2} - 4{a^2}} \over {12}}}\) \( = \sqrt {{{3{b^2} - {a^2}} \over 3}} \)
b. Kẻ AC1 ⊥ SC thì (P) chính là mp(ABC1)
Vì SAC là tam giác cân mà AC1 ⊥ SC nên C1 nằm giữa S và C khi và chỉ khi
\(\widehat {ASC} < 90^\circ \Leftrightarrow A{S^2} + C{S^2} > A{C^2} \) \(\Leftrightarrow 2{b^2} > {a^2}\)
Ta có : AB ⊥ GC và AB ⊥ SG ⇒ AB ⊥ SC
SC ⊥ AC1 và SC ⊥ AB nên SC ⊥ (ABC1)
Thể tích tứ diện SABC là :
\(\eqalign{ & {V_{SABC}} = {1 \over 3}SG.{S_{ABC}} = {1 \over 3}SC.{S_{AB{C_1}}} \cr & \Rightarrow {S_{AB{C_1}}} = {{SG.{S_{ABC}}} \over {SC}} \cr &= {{\sqrt {{{3{b^2} - {a^2}} \over 3}} .{{{a^2}\sqrt 3 } \over 4}} \over b} = {{{a^2}\sqrt {3{b^2} - {a^2}} } \over {4b}} \cr} \)
Câu 19 trang 103 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học 11, tập trung vào việc vận dụng kiến thức về vectơ trong không gian để giải quyết các bài toán liên quan đến hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ (cộng, trừ, nhân với một số thực), và các tính chất của vectơ.
Trước khi bắt đầu giải bài toán, điều quan trọng là phải đọc kỹ đề bài và xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, đề bài sẽ cung cấp thông tin về một hình hình học nào đó (ví dụ: hình hộp, hình chóp, hình lăng trụ) và yêu cầu tính toán một đại lượng nào đó liên quan đến hình đó (ví dụ: độ dài cạnh, góc giữa hai đường thẳng, khoảng cách giữa hai mặt phẳng).
Để giải Câu 19 trang 103 SGK Hình học 11 Nâng cao, học sinh có thể áp dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết của bài toán Câu 19 trang 103 SGK Hình học 11 Nâng cao. Lời giải này sẽ bao gồm các bước giải cụ thể, các phép tính chi tiết, và các giải thích rõ ràng để học sinh có thể hiểu được cách giải bài toán.)
Để giúp học sinh hiểu rõ hơn về cách giải bài toán, chúng ta có thể xem xét một ví dụ minh họa cụ thể. Ví dụ, nếu bài toán yêu cầu tính góc giữa hai đường thẳng AB và CD, chúng ta có thể sử dụng công thức tính góc giữa hai đường thẳng thông qua tích vô hướng của hai vectơ chỉ phương của hai đường thẳng đó.
Ngoài việc giải Câu 19 trang 103 SGK Hình học 11 Nâng cao, học sinh có thể tìm hiểu thêm về các ứng dụng của vectơ trong hình học, ví dụ như trong việc giải các bài toán về hình chiếu, hình đối xứng, và hình đồng dạng. Việc nắm vững kiến thức về vectơ sẽ giúp học sinh giải quyết các bài toán hình học một cách hiệu quả và sáng tạo hơn.
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự như Câu 19 trang 103 SGK Hình học 11 Nâng cao. Các bài tập này có thể được tìm thấy trong sách giáo khoa, sách bài tập, hoặc trên các trang web học toán online.
Câu 19 trang 103 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Bằng cách nắm vững các khái niệm cơ bản, áp dụng các phương pháp giải phù hợp, và luyện tập thường xuyên, học sinh có thể tự tin giải quyết bài toán này và các bài toán tương tự một cách hiệu quả.