Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
Tính các góc của tam giác ABC
Đề bài
Tính các góc của tam giác \(ABC\), biết \(AB = \sqrt 2 cm\), \(AC =\sqrt 3 cm\) và đường cao \(AH = 1cm\). (Gợi ý : Xét trường hợp \(B, C\) nằm khác phía đối với \(H\) và trường hợp \(B, C\) nằm cùng phía đối với \(H\)).
Lời giải chi tiết
Ta xét hai trường hợp :
a/ \(B\) và \(C\) nằm khác phía đối với \(H\)
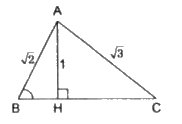
Trong tam giác vuông \(ABH\) ta có :
\(\sin B = {{AH} \over {AB}} = {1 \over {\sqrt 2 }}\)
Suy ra \(\widehat B = 45^\circ \) (chú ý rằng góc \(B\) nhọn)
Trong tam giác \(ACH\) ta có :
\(\sin C = {{AH} \over {AC}} = {1 \over {\sqrt 3 }},\) suy ra \(\widehat C \approx 35^\circ 15'52\)
Từ đó \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) \approx 99^\circ 44'8\)
b/ \(B\) và \(C\) nằm cùng phía đối với \(H\)

Tương tự như trên ta có:
\(\sin \widehat {ABH} = \frac{{AH}}{{AB}} = \frac{1}{{\sqrt 2 }}\) \( \Rightarrow \widehat {ABH} = {45^0}\)
\(\eqalign{& \widehat {ABC} = 180^\circ - \widehat {ABH} \cr&= 180^\circ - 45^\circ = 135^\circ \cr } \)
\(\sin \widehat {ACH} = \frac{{AH}}{{AC}} = \frac{1}{{\sqrt 3 }}\) \( \Rightarrow \widehat {ACH} = {35^0}15'52''\)
Từ đó \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) \approx 9^\circ 44'8\)
Câu 22 trang 30 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học kỳ I, lớp 11. Bài toán này thường liên quan đến việc xác định tính đơn điệu của hàm số, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc khảo sát hàm số.
Trước khi đi vào giải chi tiết, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu. Đọc kỹ đề, xác định hàm số được cho, khoảng xác định của hàm số, và yêu cầu cụ thể của bài toán (ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất, khoảng đơn điệu, v.v.).
Để giải quyết bài toán này, chúng ta có thể sử dụng các phương pháp sau:
(Giả sử đề bài là: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x3 - 3x2 + 2 trên đoạn [-1; 3])
Khi giải các bài tập về hàm số, cần lưu ý những điều sau:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Câu 22 trang 30 SGK Đại số và Giải tích 11 Nâng cao là một bài tập điển hình về khảo sát hàm số. Việc nắm vững phương pháp giải và rèn luyện thường xuyên sẽ giúp bạn tự tin giải quyết các bài tập tương tự.