Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Hình học 11 Nâng cao. Bài viết này sẽ tập trung vào việc giải Câu 8 trang 121 SGK Hình học 11 Nâng cao, giúp bạn hiểu rõ phương pháp và cách tiếp cận để giải quyết các bài toán tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng cao, dễ hiểu và phù hợp với nhu cầu học tập của học sinh. Hãy cùng bắt đầu với lời giải chi tiết của câu hỏi này.
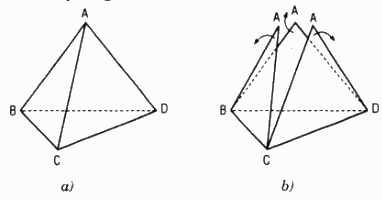
Cho tứ diện ABCD. Cắt tứ diện đó theo các cạnh đó theo các cạnh AB, AC, AD và trải các mặt ABC, ACD, ADB lên mặt phẳng (BCD) (xem hình 133). Hình phẳng gồm các tam giác BCD, A1BC, A2CD, A3BD gọi là hình khai triển của tứ diện ABCD trên mặt phẳng (BCD).
Đề bài
Cho tứ diện ABCD. Cắt tứ diện đó theo các cạnh đó theo các cạnh AB, AC, AD và trải các mặt ABC, ACD, ADB lên mặt phẳng (BCD) (xem hình 133). Hình phẳng gồm các tam giác BCD, A1BC, A2CD, A3BD gọi là hình khai triển của tứ diện ABCD trên mặt phẳng (BCD).
Lời giải chi tiết
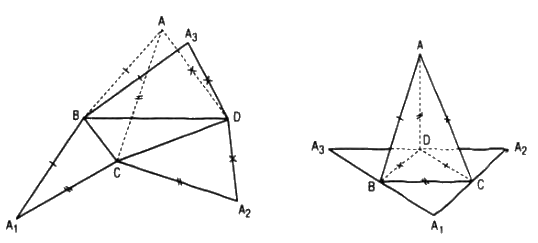
Ta có hình khai triển của tứ diện ABCD trên mp(BCD) là tam giác A1A2A3.
Ta chỉ cần chứng minh tam giác A1A2A3 có ba góc nhọn.
Thật vậy, xét tam giác AA1A2 có AC = A1C = A2C nên AA1 ⊥ AA2. Lí luận tương tự như trên, ta có AA1, AA2, AA3 đôi một vuông góc, từ đó tứ diện AA1A2A3 có mặt A1A2A3 là tam giác có ba góc nhọn.
Câu 8 trang 121 SGK Hình học 11 Nâng cao thường liên quan đến các kiến thức về vectơ, đặc biệt là các phép toán vectơ trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các khái niệm cơ bản như:
Trước khi bắt tay vào giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu tính toán một giá trị nào đó liên quan đến vectơ, hoặc chứng minh một đẳng thức vectơ. Dưới đây là một số phương pháp giải thường được sử dụng:
(Giả sử đề bài Câu 8 trang 121 SGK Hình học 11 Nâng cao là: Cho hai vectơ a = (1; 2; 3) và b = (-2; 1; 0). Tính tích vô hướng của a và b.)
Lời giải:
Tích vô hướng của hai vectơ a = (x1; y1; z1) và b = (x2; y2; z2) được tính theo công thức:
a.b = x1x2 + y1y2 + z1z2
Trong trường hợp này, ta có:
a.b = (1)(-2) + (2)(1) + (3)(0) = -2 + 2 + 0 = 0
Vậy, tích vô hướng của hai vectơ a và b là 0.
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, bạn nên luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tìm hiểu thêm về các ứng dụng của vectơ trong hình học không gian, chẳng hạn như:
Câu 8 trang 121 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài tập về vectơ. Bằng cách nắm vững các khái niệm cơ bản, phương pháp giải và luyện tập thường xuyên, bạn sẽ có thể tự tin giải quyết các bài toán tương tự một cách hiệu quả.
Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về Câu 8 trang 121 SGK Hình học 11 Nâng cao. Chúc bạn học tập tốt!