Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và mối quan hệ giữa các vectơ để giải quyết các bài toán liên quan đến hình học không gian.
giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.
Cho hình chóp S.ABCD có đáy là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua O, song song với AB và SC. Thiết diện đó là hình gì ?
Đề bài
Cho hình chóp S.ABCD có đáy là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua O, song song với AB và SC. Thiết diện đó là hình gì ?
Lời giải chi tiết
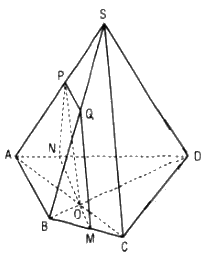
Gọi (α) là mặt phẳng qua O song song với AB và SC.
AB // (α) nên (α) cắt mp(ABCD) theo giao tuyến qua O và song song với AB. Gọi M, N lần lượt là giao điểm của đường thẳng qua O song song AB với BC và AD.
Trong mặt phẳng (SAC) kẻ OP // SC (P ϵ AS) (α) cắt mp(SAB) theo giao tuyến PQ // AB (Q ϵ SB)
Thiết diện cần tìm là tứ giác MNPQ.
Tứ giác MNPQ có PQ // MN nên MNPQ là hình thang.
Bài toán Câu 27 trang 60 SGK Hình học 11 Nâng cao thường thuộc dạng bài tập về vectơ trong không gian, cụ thể là việc chứng minh các đẳng thức vectơ hoặc xác định mối quan hệ giữa các điểm trong không gian thông qua vectơ. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Để cung cấp một lời giải cụ thể, chúng ta cần biết nội dung chính xác của bài toán Câu 27 trang 60. Tuy nhiên, dựa trên kinh nghiệm giảng dạy và phân tích các bài tập tương tự, chúng ta có thể đưa ra một phương pháp giải tổng quát:
Giả sử bài toán yêu cầu chứng minh rằng bốn điểm A, B, C, D là đồng phẳng. Chúng ta có thể sử dụng phương pháp vectơ để giải quyết bài toán này như sau:
1. Biểu diễn các vectơ:\overrightarrow{AB}", "\overrightarrow{AC}", "\overrightarrow{AD}" bằng tọa độ.
2. Tính tích hỗn hợp: Tính tích hỗn hợp \overrightarrow{AB} \cdot (\overrightarrow{AC} \times \overrightarrow{AD}).
3. Kết luận: Nếu tích hỗn hợp bằng 0, thì bốn điểm A, B, C, D đồng phẳng.
Ngoài bài toán Câu 27 trang 60, học sinh có thể gặp các dạng bài tập tương tự liên quan đến vectơ trong không gian, bao gồm:
Để giải các bài toán về vectơ trong không gian một cách hiệu quả, học sinh nên:
Học sinh có thể tham khảo thêm các tài liệu sau để nắm vững kiến thức về vectơ trong không gian:
Câu 27 trang 60 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp học sinh củng cố kiến thức về vectơ trong không gian. Bằng cách nắm vững các kiến thức cơ bản, luyện tập thường xuyên và áp dụng các phương pháp giải phù hợp, học sinh có thể tự tin giải quyết bài toán này và các bài toán tương tự.