Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Hình học 11 Nâng cao.
Trong bài viết này, chúng tôi sẽ cùng nhau giải quyết Câu 9 trang 126 SGK Hình học 11 Nâng cao, giúp bạn hiểu rõ hơn về kiến thức và phương pháp giải bài tập liên quan.
Hãy cùng bắt đầu với lời giải chi tiết và những lưu ý quan trọng để nắm vững kiến thức Hình học 11 Nâng cao nhé!
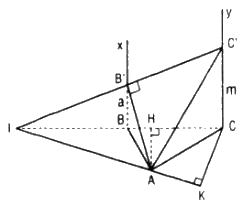
Cho tam giác ABC vuông tại A, AB = a, BC = 2a. Hai tia Bx và Cy cùng vuông góc với mp(ABC) và nằm về một phía đối với mặt phẳng đó. Trên Bx, Cy lần lượt lấy các điểm B’, C’ sao cho BB’ = a, CC’ = m.
Đề bài
Cho tam giác ABC vuông tại A, AB = a, BC = 2a. Hai tia Bx và Cy cùng vuông góc với mp(ABC) và nằm về một phía đối với mặt phẳng đó. Trên Bx, Cy lần lượt lấy các điểm B’, C’ sao cho BB’ = a, CC’ = m.
a. Với giá trị nào của m thì AB’C’ là tam giác vuông ?
b. Khi tam giác AB’C’ vuông tại B’, kẻ AH ⊥ BC. Chứng minh rằng B’C’H là tam giác vuông. Tính góc giữa hai mặt phẳng (ABC) và (AB’C’).
Lời giải chi tiết
\(\Delta ABC\) vuông tại A nên theo pitago:
\(A{C^2} = B{C^2} - A{B^2}\) \( = {\left( {2a} \right)^2} - {a^2} = 3{a^2}\)
Tam giác ABB’ vuông tại B nên theo pitago:
\(AB{'^2} = A{B^2} + BB{'^2}\) \( = {a^2} + {a^2} = 2{a^2}\)
Tam giác ACC’ vuông tại C nên theo pitago:
\(AC{'^2} = A{C^2} + CC{'^2} = 3{a^2} + {m^2}\)
Trong (BCC’B’), kẻ \(B'M \bot CC'\) thì \(B'M = 2a,MC' = m - a\)
Tam giác B’MC’ vuông tại M nên theo pitago:
\(B'C{'^2} = B'{M^2} + MC{'^2}\) \( = {\left( {2a} \right)^2} + {\left( {m - a} \right)^2} = 4{a^2} + {\left( {m - a} \right)^2}\)
a. Ta có:
+) Tam giác AB’C’ vuông ở A khi và chỉ khi:
\(\begin{array}{l}AB{'^2} + AC{'^2} = B'C{'^2}\\ \Leftrightarrow 2{a^2} + 3{a^2} + {m^2} = 4{a^2} + {\left( {m - a} \right)^2}\\ \Leftrightarrow 5{a^2} + {m^2} = 4{a^2} + {m^2} - 2ma + {a^2}\\ \Leftrightarrow 2ma = 0\\ \Leftrightarrow m = 0\end{array}\)
Vậy tam giác AB’C’ vuông ở A khi và chỉ khi m = 0
+) Tam giác AB’C’ vuông ở C’ khi và chỉ khi :
\(\begin{array}{l}AC{'^2} + B'C{'^2} = AB{'^2}\\ \Leftrightarrow 3{a^2} + {m^2} + 4{a^2} + {\left( {m - a} \right)^2} = 2{a^2}\\ \Leftrightarrow 5{a^2} + {m^2} + {\left( {m - a} \right)^2} = 0\end{array}\)
Điều này không xảy ra vì:
\(\left\{ \begin{array}{l}5{a^2} > 0\\{m^2} \ge 0\\{\left( {m - a} \right)^2} \ge 0\end{array} \right.\)\( \Rightarrow 5{a^2} + {m^2} + {\left( {m - a} \right)^2} > 0,\forall m\)
Tam giác AB’C’ vuông ở B’ khi và chỉ khi :
\(\begin{array}{l}AB{'^2} + B'C{'^2} = AC{'^2}\\ \Leftrightarrow 2{a^2} + 4{a^2} + {\left( {m - a} \right)^2} = 3{a^2} + {m^2}\\ \Leftrightarrow 6{a^2} + {m^2} - 2ma + {a^2} - 3{a^2} - {m^2} = 0\\ \Leftrightarrow 4{a^2} - 2ma = 0\\ \Leftrightarrow 2ma = 4{a^2}\\ \Leftrightarrow m = 2a\end{array}\)
Vậy tam giác AB’C’ vuông ở B’ khi và chỉ khi m = 2a
b. Giả sử tam giác AB’C’ vuông ở B’, tức là m = 2a
Tam giác ABC vuông tại A có đường cao AH nên:
\(BH.BC = A{B^2}\)\( \Leftrightarrow BH = \frac{{A{B^2}}}{{BC}} = \frac{{{a^2}}}{{2a}} = \frac{a}{2}\)
\( \Rightarrow HC = BC - BH\) \( = 2a - \frac{a}{2} = \frac{{3a}}{2}\)
Tam giác B’BH vuông tại B nên:
\(B'{H^2} = B'{B^2} + B{H^2}\) \( = {a^2} + {\left( {\frac{a}{2}} \right)^2} = \frac{{5{a^2}}}{4}\)
Tam giác C’CH vuông tại C nên:
\(C'{H^2} = C'{C^2} + C{H^2}\) \( = {\left( {2a} \right)^2} + {\left( {\frac{{3a}}{2}} \right)^2} = \frac{{25{a^2}}}{4}\)
\(B'C{'^2} = 4{a^2} + {\left( {2a - a} \right)^2} = 5{a^2}\)
\( \Rightarrow B'{H^2} + B'C{'^2}\) \( = \frac{{5{a^2}}}{4} + 5{a^2} = \frac{{25{a^2}}}{4} = C'{H^2}\)
\( \Rightarrow \Delta B'C'H\) vuông tại B’.
*) Tính góc giữa mp(ABC) và mp(AB’C’) khi m = 2a.
Gọi I là giao điểm của B’C’ và BC.
Do BB’ // CC’ , BB’ = a, CC’ = 2a nên BB' là đường trung bình của tam giác ICC'
Do đó BC = BI, B’C’ = B’I.
Xét phép chiếu lên mp(ABC). Ta có tam giác AIC là hình chiếu của tam giác AIC’. Gọi φ là góc giữa mp(ABC) và mp(AB’C’) thì \({S_{AIC}} = {S_{AIC'}}\cos \varphi \)
Ta có: \({S_{AIC}} = 2{S_{ABC}} \)\( = 2.\frac{1}{2}AB.AC = 2.\frac{1}{2}.a.a\sqrt 3 = {a^2}\sqrt 3 \)
Mặt khác : \({S_{AIC'}} = {1 \over 2}IC'.AB' \)\(= {1 \over 2}.2a\sqrt 5 .a\sqrt 2 = {a^2}\sqrt {10} \)
Từ đó : \(\cos \varphi = {{{a^2}\sqrt 3 } \over {{a^2}\sqrt {10} }} = {{\sqrt {30} } \over {10}}\)
Vậy góc giữa mp(ABC) và mp(AB’C’) là φ được tính bởi \(\cos \varphi = {{\sqrt {30} } \over {10}},0^\circ < \varphi < 90^\circ \)
.
Câu 9 trang 126 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về vectơ, đặc biệt là các phép toán vectơ như cộng, trừ, nhân với một số thực và tích vô hướng để giải quyết bài toán liên quan đến hình học không gian. Bài toán thường liên quan đến việc chứng minh các đẳng thức vectơ, xác định mối quan hệ giữa các vectơ, hoặc tính độ dài của vectơ.
Trước khi bắt đầu giải, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Điều này giúp chúng ta lựa chọn phương pháp giải phù hợp và tránh sai sót trong quá trình giải.
Để giải Câu 9 trang 126, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Có nhiều phương pháp giải bài toán vectơ, tùy thuộc vào yêu cầu cụ thể của bài toán. Một số phương pháp thường được sử dụng bao gồm:
(Giả sử đề bài cụ thể của Câu 9 là: Cho hình hộp ABCD.A'B'C'D'. Gọi I là trung điểm của AB. Chứng minh rằng: overrightarrow{CI} vuông góc với overrightarrow{A'B'})
Lời giải:
Gọi O là trung điểm của CD. Ta có:
Sử dụng các tính chất của vectơ và hình hộp, ta có thể chứng minh overrightarrow{CI} . overrightarrow{A'B'} = 0, suy ra overrightarrow{CI} vuông góc với overrightarrow{A'B'}.
Để giải bài toán vectơ một cách hiệu quả, bạn cần lưu ý những điều sau:
Để củng cố kiến thức và kỹ năng giải bài toán vectơ, bạn nên luyện tập thêm với các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và tự tin hơn khi giải các bài toán khó.
Câu 9 trang 126 SGK Hình học 11 Nâng cao là một bài toán điển hình về ứng dụng của vectơ trong hình học không gian. Việc giải bài toán này đòi hỏi chúng ta phải nắm vững các kiến thức cơ bản về vectơ và lựa chọn phương pháp giải phù hợp. Hy vọng rằng, với lời giải chi tiết và những lưu ý quan trọng mà chúng tôi đã cung cấp, bạn sẽ hiểu rõ hơn về bài toán này và tự tin hơn khi giải các bài toán tương tự.