Chào mừng bạn đến với bài giải chi tiết Câu 2 trang 120 SGK Hình học 11 Nâng cao trên giaitoan.edu.vn. Bài tập này thuộc chương trình Hình học không gian, tập trung vào việc vận dụng kiến thức về vectơ và các phép toán liên quan.
Chúng tôi cung cấp lời giải dễ hiểu, phương pháp giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S.ABC có SA = Sb = SC = a,
Đề bài
Cho hình chóp S.ABC có SA = SB = SC = a, \(\widehat {ASB} = 120^\circ ,\widehat {BSC} = 60^\circ ,\widehat {CSA} = 90^\circ \) .
a. Chứng tỏ rằng ABC là tam giác vuông
b. Tính khoảng cách từ S đến mặt phẳng (ABC)
Lời giải chi tiết
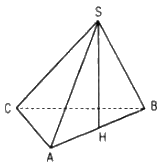
a. Ta có:
\(\eqalign{ & \overrightarrow {CA} .\overrightarrow {CB} \cr &= \left( {\overrightarrow {SA} - \overrightarrow {SC} } \right)\left( {\overrightarrow {SB} - \overrightarrow {SC} } \right) \cr & = \overrightarrow {SA} .\overrightarrow {SB} - \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SC} .\overrightarrow {SB} + S{C^2} \cr & = {a^2}\cos 120^\circ - {a^2}\cos 90^\circ - {a^2}\cos 60^\circ + {a^2} \cr & = {a^2} - {{{a^2}} \over 2} - {{{a^2}} \over 2} = 0 \cr & \Rightarrow CA \bot CB \cr} \)
⇒ ΔABC vuông tại C.
b. Kẻ SH ⊥ mp(ABC), do SA = SB = SC nên HA = HB = HC mà ΔABC vuông tại C nên H là trung điểm của AB.
Áp dụng định lí cô sin vào tam giác ABC, ta có:
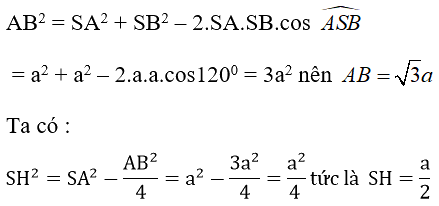
Câu 2 trang 120 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về vectơ, đặc biệt là các phép toán cộng, trừ, nhân với một số thực và tích vô hướng của hai vectơ. Bài tập này thường yêu cầu học sinh chứng minh một đẳng thức vectơ hoặc tìm một vectơ thỏa mãn một điều kiện cho trước.
(Đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: overrightarrow{AB} + vecd{AD} + vecd{AA'} = vecd{AC'})
Để giải quyết bài tập này, chúng ta cần nắm vững các kiến thức sau:
Phương pháp giải thường là sử dụng quy tắc hình bình hành, quy tắc tam giác, hoặc các tính chất của tích vô hướng để biến đổi và chứng minh đẳng thức vectơ.
(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước biến đổi, chứng minh và giải thích rõ ràng. Ví dụ:)
Ta có: overrightarrow{AB} + vecd{AD} = vecd{AC} (quy tắc hình bình hành)
Lại có: vecd{AC} + vecd{AA'} = vecd{AC'}
Do đó: overrightarrow{AB} + vecd{AD} + vecd{AA'} = vecd{AC'} (đpcm)
Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự sau:
Kiến thức về vectơ có ứng dụng rất lớn trong Hình học không gian, đặc biệt là trong việc:
Hy vọng bài giải chi tiết Câu 2 trang 120 SGK Hình học 11 Nâng cao này sẽ giúp bạn hiểu rõ hơn về kiến thức vectơ và tự tin giải các bài tập tương tự. Chúc bạn học tốt!