Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và ứng dụng vào hình học không gian.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho tứ diện ABCD và ba điểm P, Q, R lần lượt nằm trên ba cạnh AB, CD, BC. Hãy xác định giao điểm S của mp(PQR) với cạnh AD nếu:
PR // AC
Phương pháp giải:
- Tìm giao tuyến của (PQR) với (ACD).
Sử dụng tính chất: Nếu hai mặt phẳng chứa hai đường thẳng song song thì chúng cắt nhau theo giao tuyến song song với đường thẳng đã cho.
- Tìm giao điểm S của AD với giao tuyến trên.
Lời giải chi tiết:
Trường hợp PR // AC
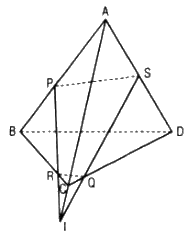
Ta có: \(\left\{ \begin{array}{l}PR \subset \left( {PQR} \right)\\AC \subset \left( {ACD} \right)\\PR//AC\\Q \in \left( {PQR} \right) \cap \left( {ACD} \right)\end{array} \right. \) \(\Rightarrow \left( {PQR} \right) \cap \left( {ACD} \right) = Qt//AC\)
Trong (ACD), gọi S = Qt ∩ AD thì S = AD ∩ (PQR).
PR cắt AC
Lời giải chi tiết:
Trường hợp PR cắt AC

Trong (ABC), gọi I = PR ∩ AC
\( \Rightarrow \left\{ \begin{array}{l}I \in AC \subset \left( {ACD} \right)\\I \in PR \subset \left( {PQR} \right)\end{array} \right.\)\( \Rightarrow I \in \left( {ACD} \right) \cap \left( {PQR} \right)\)
Mà \( Q\in \left( {ACD} \right) \cap \left( {PQR} \right)\)
⇒ (PQR) ∩ (ACD) = QI
Trong mp(ACD) ta có
S = QI ∩ AD thì S = AD ∩ (PQR).
Bài toán Câu 20 trang 55 SGK Hình học 11 Nâng cao thường xoay quanh việc chứng minh đẳng thức vectơ, xác định mối quan hệ giữa các vectơ, hoặc tính toán các đại lượng hình học liên quan đến vectơ. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Để cung cấp một lời giải cụ thể, chúng ta cần biết nội dung chính xác của bài toán. Tuy nhiên, dưới đây là một ví dụ về cách tiếp cận và giải quyết một bài toán vectơ tương tự:
Đề bài: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: overrightarrow{AB} + vecd{AD} + vecd{AA'} = vecd{AC'}
Lời giải:
overrightarrow{AC'} = vecd{AB} + vecd{BC'} = vecd{AB} + vecd{CD} = vecd{AB} + vecd{AD} + vecd{DC} = vecd{AB} + vecd{AD} + vecd{AA'}
Vậy, overrightarrow{AB} + vecd{AD} + vecd{AA'} = vecd{AC'}.
Ngoài bài toán chứng minh đẳng thức vectơ, Câu 20 trang 55 SGK Hình học 11 Nâng cao có thể xuất hiện các dạng bài tập sau:
Để giải các bài toán vectơ một cách nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và kỹ năng giải toán, bạn có thể luyện tập thêm các bài tập sau:
Câu 20 trang 55 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng giải toán vectơ và ứng dụng vào hình học không gian. Bằng cách nắm vững kiến thức cơ bản, áp dụng các phương pháp giải phù hợp, và luyện tập thường xuyên, bạn có thể tự tin giải quyết mọi bài toán liên quan đến vectơ.