Câu 11 trang 14 SGK Hình học 11 Nâng cao

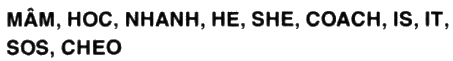
Giải Chi Tiết Câu 11 Trang 14 SGK Hình học 11 Nâng cao

Câu 11 trang 14 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học 11 Nâng cao, tập trung vào việc củng cố kiến thức về vectơ và ứng dụng của chúng trong giải quyết các bài toán hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:

• Vectơ: Định nghĩa, các phép toán cộng, trừ, nhân với một số thực.
• Tích vô hướng của hai vectơ: Công thức tính, ứng dụng để tính góc giữa hai vectơ, kiểm tra tính vuông góc.
• Hệ tọa độ: Biểu diễn vectơ trong hệ tọa độ, các phép toán vectơ trong hệ tọa độ.

Phân Tích Đề Bài

Trước khi bắt tay vào giải bài tập, việc phân tích đề bài một cách cẩn thận là vô cùng quan trọng. Hãy xác định rõ:

• Yêu cầu của đề bài: Đề bài yêu cầu chúng ta tìm gì? (ví dụ: tìm tọa độ điểm, tính độ dài đoạn thẳng, chứng minh tính vuông góc, v.v.).
• Dữ kiện đã cho: Đề bài cung cấp những thông tin gì? (ví dụ: tọa độ các điểm, phương trình đường thẳng, v.v.).
• Mối liên hệ giữa các yếu tố: Các yếu tố đã cho có mối liên hệ gì với nhau? (ví dụ: các điểm nằm trên một đường thẳng, hai vectơ vuông góc, v.v.).

Lời Giải Chi Tiết

(Giả sử đề bài là: Cho A(1;2), B(3;4), C(5;6). Tìm tọa độ điểm D sao cho ABCD là hình bình hành.)

Để giải bài toán này, ta sử dụng tính chất của hình bình hành: vectơ AB = vectơ DC.

1. Tính vectơ AB: AB = (3-1; 4-2) = (2; 2)
2. Giả sử tọa độ điểm D là (x; y): DC = (5-x; 6-y)
3. Áp dụng tính chất hình bình hành: (2; 2) = (5-x; 6-y)
4. Giải hệ phương trình:
   • 5 - x = 2 => x = 3
   • 6 - y = 2 => y = 4
5. Kết luận: Tọa độ điểm D là (3; 4)

Các Dạng Bài Tập Tương Tự

Ngoài bài tập trên, còn rất nhiều dạng bài tập tương tự liên quan đến vectơ và ứng dụng của chúng trong hình học. Một số dạng bài tập phổ biến bao gồm:

• Tìm tọa độ điểm thỏa mãn điều kiện cho trước: Ví dụ: tìm tọa độ điểm M sao cho MA + MB = 0.
• Chứng minh ba điểm thẳng hàng: Sử dụng điều kiện hai vectơ cùng phương.
• Chứng minh hai đường thẳng song song hoặc vuông góc: Sử dụng tích vô hướng của hai vectơ chỉ phương hoặc vectơ pháp tuyến.
• Tính diện tích hình bình hành, tam giác: Sử dụng công thức tính diện tích thông qua vectơ.

Mẹo Giải Bài Tập

Để giải các bài tập về vectơ một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:

• Vẽ hình: Vẽ hình giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
• Sử dụng tính chất của các phép toán vectơ: Ví dụ: tính giao hoán, kết hợp, phân phối của phép cộng vectơ.
• Biến đổi vectơ về dạng đơn giản nhất: Ví dụ: sử dụng các công thức biến đổi tọa độ.
• Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Luyện Tập Thêm

Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, bạn nên luyện tập thêm với các bài tập khác trong SGK và các tài liệu tham khảo. Ngoài ra, bạn có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.

Lưu ý: Bài giải trên chỉ là một ví dụ minh họa. Tùy thuộc vào đề bài cụ thể, bạn cần áp dụng các kiến thức và kỹ năng phù hợp để giải quyết.