Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và ứng dụng vào hình học không gian.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho tam giác ABC và mặt phẳng (P). Biết góc giữa mp(P) và mp(ABC) là φ (φ ≠ 90˚); hình chiếu của tam giác ABC trên mp(P) là tam giác A’B’C’. Chứng minh rằng
Tam giác ABC có một cạnh song song hoặc nằm trong mp(P)
Lời giải chi tiết:
Xét trường hợp tam giác ABC có một cạnh, chẳng hạn BC nằm trong mp(P). Gọi A’ là hình chiếu của A trên mp(P).
Kẻ đường cao A’H của tam giác A’BC (H ϵ BC) thì AH là đường cao của tam giác ABC và \(\widehat {AHA'} = \varphi ,A'H = AH\cos \varphi .\)
Ta có: \({S_{A'BC}} = {1 \over 2}BC.A'H \) \(= {1 \over 2}BC.AH\cos \varphi = {S_{ABC.cos\varphi }}\)
Trường hợp cạnh BC của tam giác ABC song song với mp(P). Xét mp(Q) chứa BC và song song với mp(P), gọi giao điểm của AA’ với mp(Q) là A1. Khi đó ta có ΔA1BC = ΔA’B’C’ ; góc giữa mp(ABC) và mp(Q) bằng φ.
Do đó : \({S_{A'B'C'}} = {S_{{A_1}BC}} = {S_{ABC }.\cos \varphi}\)
Tam giác ABC không có cạnh nào song song hay nằm trong mp(P).
Lời giải chi tiết:

Xét trường hợp tam giác ABC không có cạnh nào song song hay nằm trong mp(P).
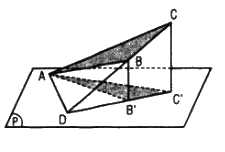
Ta có thể giả sử mp(P) đi qua điểm A sao cho các đỉnh B, C ở về cùng một phía đối với mp(P).
Gọi D là giao điểm của đường thẳng BC và mp(P); B’, C’ lần lượt là hình chiếu của B, C trên (P) thì B’C’ đi qua D.
Khi đó theo trường hợp a ta có :
\(\eqalign{ & {S_{ADC'}} = {S_{ADC.\cos \varphi }} \cr & {S_{ADB'}} = {S_{ABD.\cos \varphi }} \cr} \)
Trừ từng vế hai đẳng thức trên, ta có :
\({S_{AB'C'}} = {S_{ABC.\cos \varphi }}\)
Vậy mọi trường hợp ta đều có :
\({S_{A'B'C'}} = {S_{ABC.\cos \varphi }}\)
Câu 28 trang 112 SGK Hình học 11 Nâng cao thường thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Trước khi bắt tay vào giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài toán sẽ cho trước một số vectơ hoặc các yếu tố hình học liên quan. Nhiệm vụ của bạn là sử dụng các kiến thức đã học để tìm ra các vectơ cần tìm, tính toán các giá trị cần thiết, hoặc chứng minh một đẳng thức nào đó.
Để minh họa, chúng ta sẽ xét một ví dụ cụ thể về Câu 28 trang 112 SGK Hình học 11 Nâng cao (ví dụ này chỉ mang tính chất minh họa, đề bài thực tế có thể khác):
Đề bài: Cho hình hộp ABCD.A'B'C'D'. Gọi M là trung điểm của cạnh AB. Chứng minh rằng vectơ MM' vuông góc với mặt phẳng (ABCD).
Lời giải:
Ngoài bài toán chứng minh vectơ vuông góc với mặt phẳng, Câu 28 trang 112 SGK Hình học 11 Nâng cao và các bài tập tương tự có thể xuất hiện dưới nhiều dạng khác nhau, bao gồm:
Để giải tốt các bài toán về vectơ, bạn nên:
Câu 28 trang 112 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng vào hình học không gian. Hy vọng với lời giải chi tiết và các gợi ý trên, bạn sẽ tự tin giải quyết bài toán này và các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!