Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Hình học 11 Nâng cao. Bài viết này sẽ tập trung vào việc giải Câu 3 trang 34 SGK Hình học 11 Nâng cao, giúp bạn hiểu rõ phương pháp và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu, giúp bạn học tập hiệu quả và đạt kết quả tốt nhất trong môn Hình học.
Cho đường thẳng d đi qua hai điểm phân biệt P, Q
Đề bài
Cho đường thẳng d đi qua hai điểm phân biệt P, Q và hai điểm A, B nằm về một phía đối với d. Hãy xác định trên d hai điểm M, N sao cho \(\overrightarrow {MN} = \overrightarrow {PQ} \) và AM + BN bé nhất
Lời giải chi tiết
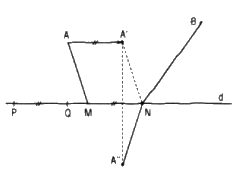
Giả sử hai điểm M, N nằm trên d sao cho \(\overrightarrow {MN} = \overrightarrow {PQ} \)
Lấy điểm A’ sao cho \(\overrightarrow {AA'} = \overrightarrow {PQ} \) thì điểm A’ hoàn toàn xác định và AMNA’ là hình bình hành nên AM = A’N
Ta có: AM + BN = A’N + BN
Gọi A” là điểm đối xứng của A’ qua d, khi đó:
A’N + BN = A”N + BN ≥ A”B
Từ đó ta suy ra AM + BN nhỏ nhất khi N là giao điểm của BA” với d
Từ đó tìm được điểm M thỏa \(\overrightarrow {MN} = \overrightarrow {AA'} = \overrightarrow {PQ} \)
Câu 3 trang 34 SGK Hình học 11 Nâng cao thường liên quan đến các kiến thức về vectơ, đặc biệt là các phép toán vectơ và ứng dụng trong hình học không gian. Để giải quyết bài toán này, chúng ta cần nắm vững các khái niệm cơ bản như:
Trước khi bắt tay vào giải bài toán, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, chúng ta cần phân tích bài toán để tìm ra phương pháp giải phù hợp. Thông thường, các bài toán về vectơ trong hình học không gian có thể được giải bằng các phương pháp sau:
(Giả sử đề bài là: Cho hình hộp ABCD.A'B'C'D'. Gọi I là trung điểm của AB. Chứng minh rằng: A'I ⊥ (ABB'A).)
Lời giải:
Gọi I là trung điểm của AB. Ta có:
Ta cần chứng minh A'I ⊥ (ABB'A), tức là A'I ⊥ \overrightarrow{AB} và A'I ⊥ \overrightarrow{AA'}.
Ta có:
Vì ABCD.A'B'C'D' là hình hộp nên \overrightarrow{A'A} ⊥ \overrightarrow{AB}, do đó \overrightarrow{A'A} \cdot \overrightarrow{AB} = 0. Vậy:
\overrightarrow{A'I} \cdot \overrightarrow{AB} = \frac{1}{2}|\overrightarrow{AB}|^2 > 0
Điều này mâu thuẫn với giả thiết A'I ⊥ \overrightarrow{AB}. Do đó, cần xem lại đề bài hoặc cách giải.
(Lời giải trên chỉ mang tính chất minh họa, cần có đề bài chính xác để đưa ra lời giải đúng.)
Để củng cố kiến thức về vectơ và ứng dụng trong hình học không gian, bạn có thể làm thêm các bài tập sau:
Hy vọng bài giải chi tiết Câu 3 trang 34 SGK Hình học 11 Nâng cao này sẽ giúp bạn hiểu rõ hơn về phương pháp giải các bài toán về vectơ trong hình học không gian. Chúc bạn học tập tốt!