Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Hình học 11 Nâng cao. Bài viết này sẽ tập trung vào việc giải Câu 4 trang 34 SGK Hình học 11 Nâng cao, giúp bạn hiểu rõ phương pháp và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất, kèm theo các ví dụ minh họa để bạn có thể nắm vững kiến thức.
Cho vecto
Đề bài
Cho vecto \(\overrightarrow u \) và điểm O. Với điểm M bất kì, ta gọi M1là điểm đối xứng với M qua O và M’ là điểm sao cho \(\overrightarrow {{M_1}M'} = \overrightarrow u \). Gọi F là phép biến hình biến M thành M’
a. F là phép hợp thành của hai phép nào ? F có phải là phép dời hình hay không?
b. Chứng tỏ rằng F là một phép đối xứng tâm
Lời giải chi tiết
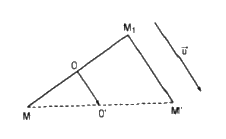
a. F là hợp thành của hai phép: phép đối xứng tâm ĐOvới tâm O và phép tịnh tiến T theo vecto \(\overrightarrow u \). Ta có F là phép dời hình vì ĐO và T là phép dời hình
b. Giả sử M1 = ĐO(M) và M’ = \(T_{\overrightarrow u }\)(M1)
Nếu gọi O’ là trung điểm của MM’ thì:
\(\overrightarrow {OO'} = {{\overrightarrow {{M_1}M'} } \over 2} = {{\overrightarrow u } \over 2}\)
Vậy điểm O’ cố định và F chính là phép đối xứng qua tâm O’
Câu 4 trang 34 SGK Hình học 11 Nâng cao thường liên quan đến các kiến thức về vectơ trong không gian, đặc biệt là các phép toán vectơ như cộng, trừ, nhân với một số thực, và tích vô hướng. Để giải quyết bài toán này, học sinh cần nắm vững các định nghĩa, tính chất và công thức liên quan đến vectơ.
Trước khi đi vào giải chi tiết, chúng ta cùng ôn lại một số kiến thức cơ bản:
Để giải Câu 4 trang 34, chúng ta cần phân tích đề bài một cách cẩn thận để xác định các vectơ liên quan và các mối quan hệ giữa chúng. Sau đó, áp dụng các công thức và tính chất đã học để tìm ra kết quả.
Ví dụ minh họa (giả định đề bài): Cho hình hộp ABCD.A'B'C'D'. Gọi M là trung điểm của cạnh AB. Chứng minh rằng vectơ CM vuông góc với vectơ A'M.
Ngoài Câu 4 trang 34, còn rất nhiều bài tập tương tự liên quan đến vectơ trong không gian. Để giải quyết các bài tập này, bạn có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ trong không gian, bạn nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Hãy chú trọng vào việc hiểu rõ bản chất của bài toán và áp dụng các công thức, tính chất một cách linh hoạt.
Câu 4 trang 34 SGK Hình học 11 Nâng cao là một bài tập điển hình về vectơ trong không gian. Việc giải bài tập này đòi hỏi bạn phải nắm vững các kiến thức cơ bản về vectơ, các phép toán vectơ và tích vô hướng. Hy vọng rằng, với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, bạn sẽ tự tin hơn khi đối mặt với các bài tập tương tự.
Chúc bạn học tốt!